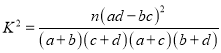Question

【题目】如图，在平面直角坐标系中，以原点为圆心，单位长度为半径的圆上有两点A（ ， ），B（ ， ）． （Ⅰ）求 ， 夹角的余弦值；
（Ⅱ）已知C（1，0），记∠AOC=α，∠BOC=β，求tan 的值．

Answer 1

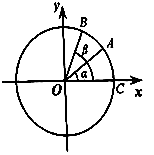
【答案】解：（Ⅰ）在平面直角坐标系中，以原点为圆心，单位长度为半径的圆上有两点 A（ ， ），B（ ， ），
∴ =（ ， ）， =（ ， ），| |=| |=1，
∴ ， 夹角的余弦值cos∠AOB= = = ．
（Ⅱ）设∠AOB的平分线OD交单位圆于点D，则∠COD= ，
从而D（cos ，sin ），∴ =（cos ，sin ），
连接AB，可知OD⊥AB，即 =0．
∴ = ﹣ =（﹣ ， ），
∴（cos ，sin ）（﹣ ， ）=﹣ cos + sin =0，
∴tan = ．
【解析】（Ⅰ）先求出向量 ， 的坐标，再跟它们的夹角的余弦值cos∠AOB= ，计算求得结果．（Ⅱ）设∠AOB的平分线OD交单位圆于点D，则∠COD= ，求得 的坐标，根据 =0，求得tan 的值．
【考点精析】掌握数量积表示两个向量的夹角和两角和与差的正切公式是解答本题的根本，需要知道设、都是非零向量，，，是与的夹角，则；两角和与差的正切公式：．