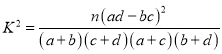题目内容
【题目】已知抛物线C:y2=2px的焦点为F,过点F且斜率为1的直线l截得圆:x2+y2=p2的弦长为2![]() .
.
(1)求抛物线C的方程;
(2)若过点F作互相垂直的两条直线l1、l2,l1与抛物线C交于A、B两点,l2与抛物线C交于D、E两点,M、N分别为弦AB、DE的中点,求|MF||NF|的最小值.
【答案】(1)y2=8x(2)32
【解析】
(1)求得抛物线C的焦点,可得直线l的方程,求得圆心(0,0)到直线的距离,由圆内的垂径定理,结合勾股定理,解方程可得p,进而得到抛物线的方程;
(2)求得焦点F的坐标,由已知可得AB⊥DE,两直线AB、DE的斜率都存在且均不为0.设直线AB的斜率为k,则直线CD的斜率为![]() ,故直线AB的方程为y=k(x﹣2).联立抛物线的方程,运用韦达定理和中点坐标公式,求得M的坐标,同理可得N的坐标,再由两点的距离公式,结合基本不等式可得所求最小值.
,故直线AB的方程为y=k(x﹣2).联立抛物线的方程,运用韦达定理和中点坐标公式,求得M的坐标,同理可得N的坐标,再由两点的距离公式,结合基本不等式可得所求最小值.
(1)由y2=2px的焦点为F(![]() ,0),
,0),
可得直线l的方程为l:y=x![]() ,
,
圆心到直线l的距离为d![]() ,
,
又d2+14=p2,可得p=4,
故抛物线C的方程为y2=8x;
(2)由(1)知焦点为F(2,0).
由已知可得AB⊥DE,所以两直线AB、DE的斜率都存在且均不为0.
设直线AB的斜率为k,则直线CD的斜率为![]() ,
,
故直线AB的方程为y=k(x﹣2).
联立方程组 ,消去x,整理得ky2﹣8y﹣16k=0,
,消去x,整理得ky2﹣8y﹣16k=0,
设点A(x1,y1),B(x2,y2),则y1+y2![]() .
.
因为M(xM,yM)为弦AB的中点,所以yM![]() (y1+y2)
(y1+y2)![]() .
.
由yM=k(xM﹣2),得xM![]() 2
2![]() 2,故点M(
2,故点M(![]() 2,
2,![]() ),
),
同理,可得N(4k2+2,﹣4k),
故|NF|![]() 4
4![]() ,
,
|MF|![]() .
.
所以|MF||NF|![]() 4
4![]() 16
16![]() 16(|k|
16(|k|![]() )
)
≥16×2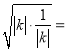 32,
32,
当且仅当|k|![]() ,即k=±1时,等号成立.
,即k=±1时,等号成立.
所以|MF||NF|的最小值为32.

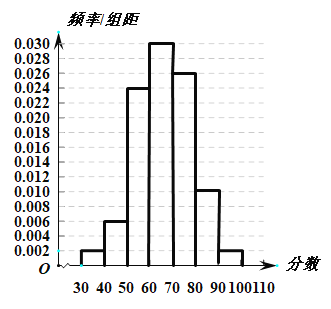
【题目】某科研团队对![]() 例新冠肺炎确诊患者的临床特征进行了回顾性分析.其中
例新冠肺炎确诊患者的临床特征进行了回顾性分析.其中![]() 名吸烟患者中,重症人数为
名吸烟患者中,重症人数为![]() 人,重症比例约为
人,重症比例约为![]() ;
;![]() 名非吸烟患者中,重症人数为
名非吸烟患者中,重症人数为![]() 人,重症比例为
人,重症比例为![]() .根据以上数据绘制
.根据以上数据绘制![]() 列联表,如下:
列联表,如下:
吸烟人数 | 非吸烟人数 | 总计 | |
重症人数 | 30 | 120 | 150 |
轻症人数 | 100 | 800 | 900 |
总计 | 130 | 920 | 1050 |
(1)根据列联表数据,能否在犯错误的概率不超过![]() 的前提下认为新冠肺炎重症和吸烟有关?
的前提下认为新冠肺炎重症和吸烟有关?
(2)已知每例重症患者平均治疗费用约为![]() 万元,每例轻症患者平均治疗费用约为
万元,每例轻症患者平均治疗费用约为![]() 万元.现有吸烟确诊患者20人,记这
万元.现有吸烟确诊患者20人,记这![]() 名患者的治疗费用总和为
名患者的治疗费用总和为![]() ,求
,求![]() .
.
附:
|
|
|
|
|
|
|
|