题目内容
已知数列{an}中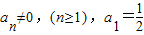 ,前n项和Sn满足:
,前n项和Sn满足: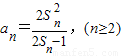
(1)求证:数列
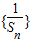 是等差数列;
是等差数列;(2)求数列{an}的通项公式;
(3)若
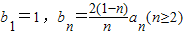 ,Sn′为数列{bn}的前n项和,求证:Sn′<2.
,Sn′为数列{bn}的前n项和,求证:Sn′<2.
【答案】分析:(1)由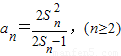 ,得Sn-Sn-1=
,得Sn-Sn-1=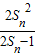 ,可化为
,可化为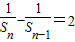 (n≥2),根据等差数列的定义可证明;
(n≥2),根据等差数列的定义可证明;
(2)由(1)可得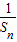 ,进而得到Sn,根据
,进而得到Sn,根据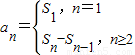 可求得an;
可求得an;
(3)表示出bn(n≥2),则S′n=b1+b2+b3+…+bn,对各项分母进行适当放缩,然后利用裂项相消法化简,可得结论;
解答:解:(1)∵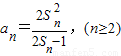 ,
,
∴Sn-Sn-1=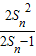 ,即
,即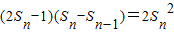 ,
,
所以Sn-1-Sn=2SnSn-1,
显然,Sn≠0,否则由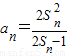 知an=0与an≠0矛盾.
知an=0与an≠0矛盾.
∴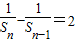 (n≥2),
(n≥2),
又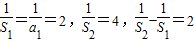 ,
,
∴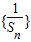 是首项为2,公差为2的等差数列;
是首项为2,公差为2的等差数列;
(2)由(1)可知: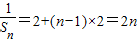 ,∴
,∴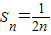 ,
,
①当n≥2时,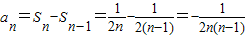 ,
,
②当n=1时,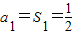 ,
,
∴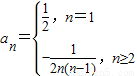 ;
;
(3)∵b1=1,且由(2)知当n≥2时,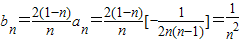 ,
,
∴S′n=b1+b2+b3+…+bn
=1+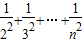
<1+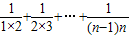
=1+(1- )+(
)+(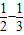 )+…+(
)+…+(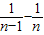 )=2-
)=2-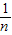 <2.
<2.
点评:本题考查数列与不等式的综合、等差数列的判定及数列求和,考查学生综合运用知识分析解决问题的能力,能力要求较高.
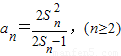 ,得Sn-Sn-1=
,得Sn-Sn-1=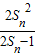 ,可化为
,可化为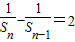 (n≥2),根据等差数列的定义可证明;
(n≥2),根据等差数列的定义可证明;(2)由(1)可得
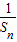 ,进而得到Sn,根据
,进而得到Sn,根据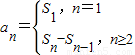 可求得an;
可求得an;(3)表示出bn(n≥2),则S′n=b1+b2+b3+…+bn,对各项分母进行适当放缩,然后利用裂项相消法化简,可得结论;
解答:解:(1)∵
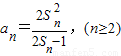 ,
,∴Sn-Sn-1=
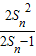 ,即
,即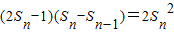 ,
,所以Sn-1-Sn=2SnSn-1,
显然,Sn≠0,否则由
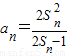 知an=0与an≠0矛盾.
知an=0与an≠0矛盾.∴
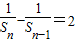 (n≥2),
(n≥2),又
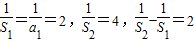 ,
,∴
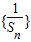 是首项为2,公差为2的等差数列;
是首项为2,公差为2的等差数列;(2)由(1)可知:
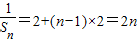 ,∴
,∴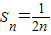 ,
,①当n≥2时,
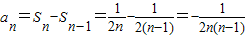 ,
,②当n=1时,
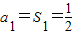 ,
,∴
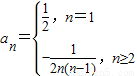 ;
;(3)∵b1=1,且由(2)知当n≥2时,
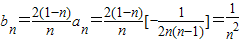 ,
,∴S′n=b1+b2+b3+…+bn
=1+
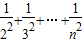
<1+
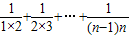
=1+(1-
 )+(
)+(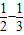 )+…+(
)+…+(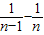 )=2-
)=2-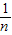 <2.
<2.点评:本题考查数列与不等式的综合、等差数列的判定及数列求和,考查学生综合运用知识分析解决问题的能力,能力要求较高.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|