题目内容
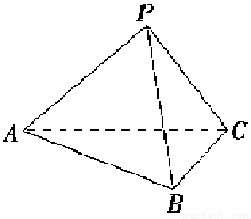
如图,已知四面体ABCD,点M、N分别是△ABC、△ACD的重心.
(1)试证:MN∥平面BCD;
(2)若∠BAC=∠CAD=∠DAB=90°,且AB=AD=1,AC=
,求证:BN⊥DM.
证明:(1)设AM、AN分别交BC、CD的中点于E、F,
因为
=
=
+
=
+
,??
所以
, 
,
共面,MN∥平面BCD.?
(2)因为
=
-
=
(
+
)-
,?
=
-
=
(
+
)-
,?
所以
·
=
|AC|2-
(|AB|2+|AD|2)=
-
=0.?
所以BN⊥DM.
练习册系列答案
相关题目
如图，已知四面体P-ABC中，PA=PB=PC，且AB=AC，∠BAC=90°，则异面直线PA与BC所成的角为
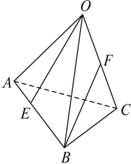
如图，已知四面体ABCD的四个面均为锐角三角形，EFGH分别是边AB，BC，CD，DA上的点，BD||平面EFGH，且EH=FG．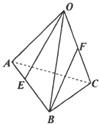
如图，已知四面体O-ABC中，E、F分别为AB，OC上的点，且AE=
AB，F为中点，若AB＝3，BC＝1，BO＝2，且∠ABC＝90°，∠OBA＝∠OBC＝60°，求异面直线OE与BF所成角的余弦值.
