题目内容
以两种饲料A和B的混合物饲养一动物.每一两饲料A中含有
解:设每份混合饲料中分别含有A种饲料x两,B种饲料y两,每份混合饲料成本z分钱,则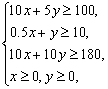 即
即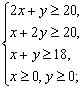
z=5x+4y.
由![]() 得
得![]()
当直线5x+4y-z=0过点(2,16)时,z的值最小.
所以每份混合饲料中A种饲料2两和B种饲料16两,才能使成本最低.

练习册系列答案
相关题目
题目内容
以两种饲料A和B的混合物饲养一动物.每一两饲料A中含有
解:设每份混合饲料中分别含有A种饲料x两,B种饲料y两,每份混合饲料成本z分钱,则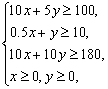 即
即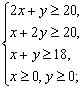
z=5x+4y.
由![]() 得
得![]()
当直线5x+4y-z=0过点(2,16)时,z的值最小.
所以每份混合饲料中A种饲料2两和B种饲料16两,才能使成本最低.
