题目内容
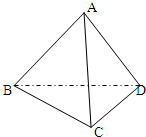（文科做）已知：如图，在空间四边形ABCD中，AB⊥CD且AC⊥BD，求证：AD⊥BC．分析：作AP垂直于平面BDC，P是垂足，连接CP，DP，BP，CP，DP，BP分别是AC，AD，AB在平面ABC内的射影，由AC⊥BD，AB⊥CD，知点P是△BDC的垂心．故DP垂直于BC．由三垂线定理，知AD⊥BC．
解答：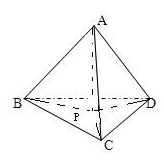
解：作AP垂直于平面BDC，P是垂足，连接CP，DP，BP，
CP，DP，BP分别是AC，AD，AB在平面BCD内的射影，
∵AC⊥BD，
∴由三垂线定理的逆定理知BD⊥CP．
∵AB⊥CD，
∴由三垂线定理的逆定理知CD⊥BP
∴点P是△BDC的垂心．
∴DP垂直于BC．
由三垂线定理，知AD⊥BC．
解：作AP垂直于平面BDC，P是垂足，连接CP，DP，BP，CP，DP，BP分别是AC，AD，AB在平面BCD内的射影，
∵AC⊥BD，
∴由三垂线定理的逆定理知BD⊥CP．
∵AB⊥CD，
∴由三垂线定理的逆定理知CD⊥BP
∴点P是△BDC的垂心．
∴DP垂直于BC．
由三垂线定理，知AD⊥BC．
点评：本题考查空间中直线与直线之间的位置关系，是基础题．解题时要认真审题，仔细解答，注意三垂线定理及其逆定理的灵活运用．
练习册系列答案
相关题目
（2011•盐城模拟）（本题文科学生做）如图，在平面直角坐标系xoy中，已知F1（-4，0），F2（4，0），A（0，8），直线y=t（0＜t＜8）与线段AF1、AF2分别交于点P、Q．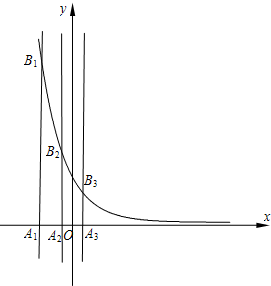
（2006•蚌埠二模）已知等差数列{an}的首项为p，公差为d（d＞0）．对于不同的自然数n，直线x=an与x轴和指数函数
