Question

正四棱锥S－ABCD中，O为底面中心，E为SA的中点，AB＝1，直线AD到平面SBC的距离等于．

（1）求斜高SM的长；

（2）求平面EBC与侧面SAD所成锐二面角的大小

Answer 1

解法一：（1）连OM，作OH⊥SM于H．

∵SM为斜高，∴M为BC的中点，∴BC⊥OM．

∵BC⊥SM，∴BC⊥平面SMO．

又OH⊥SM，∴OH⊥平面SBC．

由题意，得．

设SM＝x，

则，解之，即．

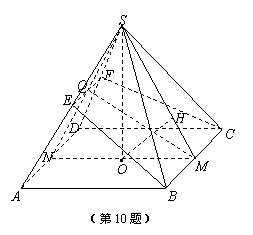
（2）设面EBC∩SD＝F，取AD中点N，连SN，设SN∩EF＝Q．

∵AD∥BC，∴AD∥面BEFC．而面SAD∩面BEFC＝EF，∴AD∥EF．

又AD⊥SN，AD⊥NM，AD⊥面SMN．

从而EF⊥面SMN，∴EF⊥QS，且EF⊥QM．

∴∠SQM为所求二面角的平面角，记为α．

由平几知识，得．

∴，∴．

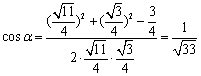∴，即　　　　　　

所求二面角为．  

解法二：（1）建立空间坐标系（如图）

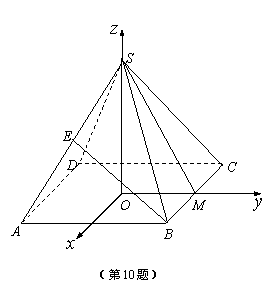
∵底面边长为1，∴，

，，

．    ……………1分

设，

平面SBC的一个法向，

则，．

∴，．

∴y＝2h，n＝（0，2h，1）．… 3分

而＝（0，1，0），由题意，得                   ．解得．

∴斜高．  

（2）n＝（0，2h，1）＝，

由对称性，面SAD的一个法向量为n₁＝．

设平面EBC的一个法向量n₂=（x，y，1），由

，，得

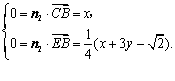 解得∴．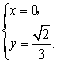

设所求的锐二面角为α，则

，∴