题目内容
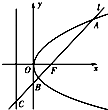如图所示，过抛物线y2=2px（p＞0）的焦点F的直线l交抛物线于点A、B，交其准线l′点C，若|BC|=2|BF|，且|AF|=3，则此抛物线的方程为（ ）分析：分别过点A，B作准线的垂线，分别交准线于点E，D，设|BF|=a，根据抛物线定义可知|BD|=a，进而推断出∠BCD的值，在直角三角形中求得a，进而根据BD∥FG，利用比例线段的性质可求得p，则抛物线方程可得．
解答：
解：如图分别过点A，B作准线的垂线，分别交准线于点E，D，设|BF|=a，则由已知得：|BC|=2a，由定义得：|BD|=a，故∠BCD=30°，
在直角三角形ACE中，∵|AE|=3，|AC|=3+3a，
∴2|AE|=|AC|
∴3+3a=6，
从而得a=1，
∵BD∥FG，
∴
=
求得p=
，
因此抛物线方程为y2=3x．
故选C．
解：如图分别过点A，B作准线的垂线，分别交准线于点E，D，设|BF|=a，则由已知得：|BC|=2a，由定义得：|BD|=a，故∠BCD=30°，在直角三角形ACE中，∵|AE|=3，|AC|=3+3a，
∴2|AE|=|AC|
∴3+3a=6，
从而得a=1，
∵BD∥FG，
∴
| 1 |
| p |
| 2 |
| 3 |
| 3 |
| 2 |
因此抛物线方程为y2=3x．
故选C．
点评：本题主要考查了抛物线的标准方程．考查了学生对抛物线的定义和基本知识的综合把握．
练习册系列答案
相关题目
设b＞0，椭圆方程为
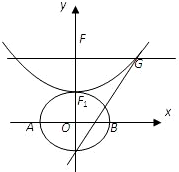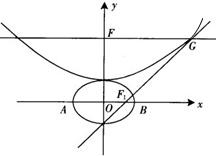
设b＞0，椭圆方程为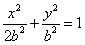
，抛物线方程为x2=8（y-b），如图所示，过点F(0，b+2)作x轴的平行线，与抛物线在第一象限的交点为G，已知抛物线在点G的切线经过椭圆的右焦点F1，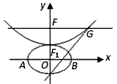
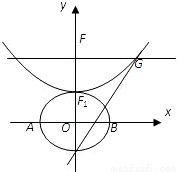
设b＞0，椭圆方程为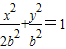
，抛物线方程为x2=8（y-b）．如图所示，过点F（0，b+2）作x轴的平行线，与抛物线在第一象限的交点为G，已知抛物线在点G的切线经过椭圆的右焦点F1．