题目内容
如图所示,过点M(m,1)作直线AB交抛物线x2=y于A,B两点,且|AM|=|MB|,过M作x轴的垂线交抛物线于点C.连接AC,BC,记三角形ABC的面积为S△,记直线AB与抛物线所围成的阴影区域的面积为S弓.
(1)求m的取值范围;
(2)当S△最大时,求m的值;
(3)是否存在常数λ,使得
=λ?若存在,求出λ的值;若不存在,请说明理由.
(1)求m的取值范围;
(2)当S△最大时,求m的值;
(3)是否存在常数λ,使得
| S△ | S弓 |
分析:(1)设AB直线方程,代入抛物线方程x2=y,利用M是AB的中点,结合根的判别式,即可求m的取值范围;
(2)利用韦达定理,表示出S△=SACM+SBCM,结合m的范围,即可求得结论;
(3)利用定积分,求出S弓,结合(2)的结论,即可求得λ的值.
(2)利用韦达定理,表示出S△=SACM+SBCM,结合m的范围,即可求得结论;
(3)利用定积分,求出S弓,结合(2)的结论,即可求得λ的值.
解答:解:(1)由题意,直线AB的斜率存在,设AB直线方程为y=k(x-m)+1
代入抛物线方程x2=y得,x2-kx+mk-1=0(*)
设A(x1,y1),B(x2,y2)
因为M是AB的中点,所以m=
=
,即k=2m
方程(*)即为:x2-2mx+2m2-1=0(**)
由△=4m2-8m2+4>0得-1<m<1
所以m的取值范围是(-1,1);…4'
(2)因为M(m,1),C(m,m2),MC⊥x轴,所以|MC|=1-m2,
由方程(**)得x1+x2=2m,x1x2=2m2-1
所以S△=SACM+SBCM=
|x1-x2| . |MC|=
. |MC|
=
. (1-m2)=(1-m2)
≤1
所以当S△最大时,m=0;…8'
(3)常数λ存在且λ=
不妨设x1<x2
S弓=
[k(x-m)+1-x2]dx=
[2mx+1-2m2-x2]dx=[mx2+(1-2m2)x-
x3]
=m(
-
)+(1-2m2)(x2-x1)-
(
-
)=(x2-x1)[m(
+
)+(1-2m2)-
(
+x2x1+
)]=(x2-x1)[m(
+
)+(1-2m2)-
((
+x1)2-x2x1)]
由方程(**)得x1+x2=2m,x1x2=2m2-1,
代入上式化简得S弓=
.
(1-m2)=
(1-m2)
由(2)知S△=(1-m2)
,所以
=
=
所以常数λ存在且λ=
…13'
代入抛物线方程x2=y得,x2-kx+mk-1=0(*)
设A(x1,y1),B(x2,y2)
因为M是AB的中点,所以m=
| x1+x2 |
| 2 |
| k |
| 2 |
方程(*)即为:x2-2mx+2m2-1=0(**)
由△=4m2-8m2+4>0得-1<m<1
所以m的取值范围是(-1,1);…4'
(2)因为M(m,1),C(m,m2),MC⊥x轴,所以|MC|=1-m2,
由方程(**)得x1+x2=2m,x1x2=2m2-1
所以S△=SACM+SBCM=
| 1 |
| 2 |
| 1 |
| 2 |
| (x1+x2)2-4x1x2 |
=
| 1 |
| 2 |
| 4-4m2 |
| 3 |
| 2 |
所以当S△最大时,m=0;…8'
(3)常数λ存在且λ=
| 3 |
| 4 |
不妨设x1<x2

S弓=
| ∫ | x2 x1 |
| ∫ | x2 x1 |
| 1 |
| 3 |
| | | x2 x1 |
| x | 2 2 |
| x | 2 1 |
| 1 |
| 3 |
| x | 3 2 |
| x | 3 1 |
| x | 2 |
| x | 1 |
| 1 |
| 3 |
| x | 2 2 |
| x | 2 1 |
| x | 2 |
| x | 1 |
| 1 |
| 3 |
| x | 2 |
由方程(**)得x1+x2=2m,x1x2=2m2-1,
代入上式化简得S弓=
| 4-4m2 |
| 2 |
| 3 |
| 4 |
| 3 |
| 3 |
| 2 |
由(2)知S△=(1-m2)
| 3 |
| 2 |
| S△ |
| S弓 |
(1-m2)
| ||||
|
| 3 |
| 4 |
所以常数λ存在且λ=
| 3 |
| 4 |
点评:本题考查直线与抛物线的位置关系,考查三角形面积的计算,考查定积分知识,考查学生的综合能力,属于中档题.

练习册系列答案
相关题目
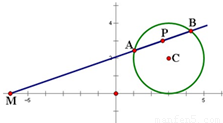
 如图所示,过点M(-6,0)作圆C:x2+y2-6x-4y+9=0的割线,交圆C于A、B两点.
如图所示,过点M(-6,0)作圆C:x2+y2-6x-4y+9=0的割线,交圆C于A、B两点. 如图所示,过点P (0,-2)的直线l交抛物线y2=4x于A,B两点,求以OA,OB为邻边的平行四边形OAMB的顶点M的轨迹方程.
如图所示,过点P (0,-2)的直线l交抛物线y2=4x于A,B两点,求以OA,OB为邻边的平行四边形OAMB的顶点M的轨迹方程.




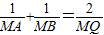 ,求点Q的轨迹.
,求点Q的轨迹.