题目内容
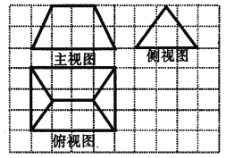
【题目】如图,已知直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的中点,点
的中点,点![]() 在直线
在直线![]() 上运动,且
上运动,且![]() .
.

(1)证明:无论![]() 取何值,总有
取何值,总有![]() 平面
平面![]() ;
;
(2)是否存在点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 的夹角为
的夹角为![]() ?若存在,试确定点
?若存在,试确定点![]() 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
【答案】(1)见解析;(2)存在点![]() ,且当
,且当![]() 时,满足平面
时,满足平面![]() 与平面
与平面![]() 的夹角为
的夹角为![]() .
.
【解析】
(1)以![]() 为正交基底建立空间直角坐标系
为正交基底建立空间直角坐标系![]() ,写出所需点的坐标,由
,写出所需点的坐标,由![]() 求出
求出![]() 点坐标,然后证明
点坐标,然后证明![]() ,
,![]() 即可;
即可;
(2)只需根据条件出平面![]() 和平面
和平面![]() 的法向量,利用向量的夹角公式并结合平面
的法向量,利用向量的夹角公式并结合平面![]() 与平面
与平面![]() 的夹角为
的夹角为![]() ,建立方程求解即可得出结论.
,建立方程求解即可得出结论.
(1)如图,以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 所在的直线分别为
所在的直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,

则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由![]() ,可得点
,可得点![]() ,
,
所以![]() ,
,![]() .
.
又![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() ,
,![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以无论![]() 取何值,总有
取何值,总有![]() 平面
平面![]() .
.
(2)设![]() 是平面
是平面![]() 的法向量,
的法向量,![]() ,
,![]() ,
,
则 ,即
,即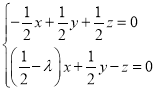 ,得
,得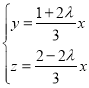 ,
,
令![]() ,所以
,所以![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
取平面![]() 的一个法向量为
的一个法向量为![]() .
.
假设存在符合条件的点![]() ,则
,则 ,
,
化简得![]() ,解得
,解得![]() 或
或![]() (舍去).
(舍去).
综上,存在点![]() ,且当
,且当![]() 时,满足平面
时,满足平面![]() 与平面
与平面![]() 的夹角为
的夹角为![]() .
.

【题目】为迎接2022年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
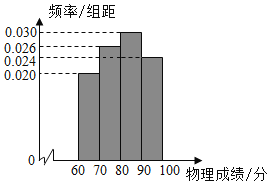
,![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
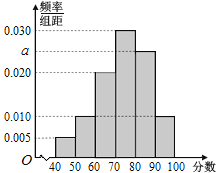
(1)求![]() 的值;
的值;
(2)估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
(3)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请将下面的2×2列联表补充完整,并判断是否有99.9%的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 | 40 | ||
女生 | 50 | ||
合计 | 100 |
参考公式及数据:![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】已知平面直角坐标系![]() ,直线
,直线![]() 过点
过点![]() ,且倾斜角为
,且倾斜角为![]() ,以
,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的参数方程和圆
的参数方程和圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的倾斜角的
的倾斜角的![]() 值.
值.
【题目】据统计,某地区植被覆盖面积![]() 公顷
公顷![]() 与当地气温下降的度数
与当地气温下降的度数![]() 之间呈线性相关关系,对应数据如下:
之间呈线性相关关系,对应数据如下:
| 20 | 40 | 60 | 80 |
| 3 | 4 | 4 | 5 |
![]() 请用最小二乘法求出y关于x的线性回归方程;
请用最小二乘法求出y关于x的线性回归方程;
![]() 根据
根据![]() 中所求线性回归方程,如果植被覆盖面积为300公顷,那么下降的气温大约是多少
中所求线性回归方程,如果植被覆盖面积为300公顷,那么下降的气温大约是多少![]() ?
?
参考公式:线性回归方程![]() ;其中
;其中![]() ,
,![]() .
.