题目内容
(2012•芜湖二模)在等差数列{an}中,a1=1,a6=2a3+1,对任意的n,设Sn=a1-a2+a3-a4+…+(-1)n-1an,则满足S2k+1>35的最小正整数K的取值等于( )
分析:由a6=2a3+1,知a1=1,d=2,an=2n-1,故Sn=1-3+5-7+…+(-1)n-1•(2n-1),由此能够求出满足S2k+1>35的最小正整数K的取值.
解答:解:∵等差数列{an}中,a1=1,a6=2a3+1,
∴
,
解得a1=1,d=2,
∴an=2n-1,
∴Sn=1-3+5-7+…+(-1)n-1•(2n-1),
∴S2k+1=S2k+(-1)2k+1-1•a2k+1=-2k+(-1)2k•a2k+1
=-2k+[2•(2k+1)-1]
=-2k+4k+1=2k+1>35,
∴2k>34,
∴k>17,
∴最小正整数K值为18,
故选C.
∴
|
解得a1=1,d=2,
∴an=2n-1,
∴Sn=1-3+5-7+…+(-1)n-1•(2n-1),
∴S2k+1=S2k+(-1)2k+1-1•a2k+1=-2k+(-1)2k•a2k+1
=-2k+[2•(2k+1)-1]
=-2k+4k+1=2k+1>35,
∴2k>34,
∴k>17,
∴最小正整数K值为18,
故选C.
点评:本题考查数列的前n项和公式的应用,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
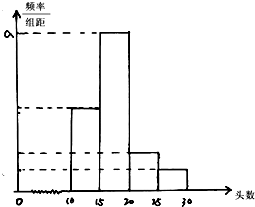 (2012•芜湖二模)某省对省内养殖场“瘦肉精”使用情况进行检查,在全省的养殖场随机抽取M个养殖场的猪作为样本,得到M个养殖场“瘦肉精”检测阳性猪的头数,根据此数据作出了频率分布表和频率分布直方图如下:
(2012•芜湖二模)某省对省内养殖场“瘦肉精”使用情况进行检查,在全省的养殖场随机抽取M个养殖场的猪作为样本,得到M个养殖场“瘦肉精”检测阳性猪的头数,根据此数据作出了频率分布表和频率分布直方图如下: