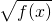题目内容
设f（x）＞0是定义在区间I上的减函数，则下列函数中增函数的个数是y=3-2f（x），y=1+
y=[f（x）]2，y=1-
（ ）A．1
B．2
C．3
D．4
【答案】分析：利用单调性的定义注意验证四个函数是否为区间I上的减函数即可，判断方法，先设定义域上任意两个x1，x2，
x1＜x2，只需再用作差法比较y1，y2的大小即可，比较时，应该借助函数f（x）＞0且是定义在区间I上的减函数．
解答：解：∵f（x）＞0且f（x）在I上是减函数，∴在区间I上任取两个x1，x2，当x1＜x2时，f（x1）＞f（x2）
对于函数y=3-2f（x），y1-y2=3-2f（x1）-3+2f（x2）=2f（x2）-2f（x1）＜0，
∴y=3-2f（x）是增函数，
对于函数y=1+
，y1-y2=1+
-1-
=
-
=
＜0
∴函数y=1+
是增函数，
对于函数y=[f（x）]2，y1-y2=[f（x1）]2-[f（x2）]2=[f（x1）+f（x2）][f（x1）-f（x2）]
∵f（x）＞0，∴y1-y2＞0，∴函数y=[f（x）]2是减函数．
对于函数y=1-
，y1-y2=1-
-1+
=
-
＜0
∴函数y=1-
为I上的增函数，
故选C．
点评：本题主要考查抽象函数单调性的证明，严格按照步骤去做，设定义域上任意两个x1，x2，x1＜x2，再用作差法比较y1，y2的大小即可．
x1＜x2，只需再用作差法比较y1，y2的大小即可，比较时，应该借助函数f（x）＞0且是定义在区间I上的减函数．
解答：解：∵f（x）＞0且f（x）在I上是减函数，∴在区间I上任取两个x1，x2，当x1＜x2时，f（x1）＞f（x2）
对于函数y=3-2f（x），y1-y2=3-2f（x1）-3+2f（x2）=2f（x2）-2f（x1）＜0，
∴y=3-2f（x）是增函数，
对于函数y=1+
，y1-y2=1+-1-=-=＜0∴函数y=1+
是增函数，对于函数y=[f（x）]2，y1-y2=[f（x1）]2-[f（x2）]2=[f（x1）+f（x2）][f（x1）-f（x2）]
∵f（x）＞0，∴y1-y2＞0，∴函数y=[f（x）]2是减函数．
对于函数y=1-
，y1-y2=1--1+=-＜0∴函数y=1-
为I上的增函数，故选C．
点评：本题主要考查抽象函数单调性的证明，严格按照步骤去做，设定义域上任意两个x1，x2，x1＜x2，再用作差法比较y1，y2的大小即可．
练习册系列答案
相关题目
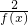y=[f（x）]2，y=1-