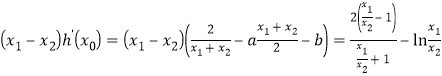题目内容
【题目】已知函数![]()
![]() .
.
(Ⅰ)当![]() 时,求
时,求![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(Ⅱ)若函数![]() 有两个不同零点
有两个不同零点![]() ,
, ![]() ,且
,且![]() ,求证:
,求证: ![]() ,其中
,其中![]() 是
是![]() 的导函数.
的导函数.
【答案】(Ⅰ)y=2x-1;(Ⅱ)证明见解析.
【解析】试题分析:(I)利用导数的几何意义即可得出![]() 的图象在
的图象在![]() 处的切线方程;(Ⅱ)由于
处的切线方程;(Ⅱ)由于![]() 的图象与
的图象与![]() 轴交于两个不同的点
轴交于两个不同的点![]() ,
, ![]() ,可得方程
,可得方程![]() 的两个根为
的两个根为![]() ,
, ![]() ,得到
,得到![]() ,可得
,可得![]() ,经过变形只要证明
,经过变形只要证明![]() ,通过换元再利用导数研究其单调性即可得出.
,通过换元再利用导数研究其单调性即可得出.
试题解析:(Ⅰ)当![]() 时,
时, ![]() ,
, ![]() ,切点坐标为
,切点坐标为![]() ,切线的斜率
,切线的斜率![]() ,∴切线方程为
,∴切线方程为![]() ,即
,即![]() .
.
(Ⅱ)∵![]() 的图象与
的图象与![]() 轴交于两个不同的点
轴交于两个不同的点![]() ,
, ![]() ,∴方程
,∴方程![]() 的两个根为
的两个根为![]() ,
, ![]() ,则
,则![]() ,两式相减得
,两式相减得![]() ,又
,又![]() ,
, ![]() ,则
,则![]() ,下证
,下证![]() (*),即证明
(*),即证明![]() ,令
,令![]() ,∵
,∵![]() ,∴
,∴![]() ,即证明
,即证明![]() 在
在![]() 上恒成立,∵
上恒成立,∵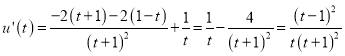 ,又
,又![]() ,∴
,∴![]() ,∴
,∴![]() 在
在![]() 上是增函数,则
上是增函数,则![]() ,从而知
,从而知![]() ,故(*)式
,故(*)式![]() ,即
,即![]() 成立.
成立.

练习册系列答案
相关题目
【题目】某校在学年期末举行“我最喜欢的文化课”评选活动,投票规则是一人一票,高一(1)班44名学生和高一(7)班45名学生的投票结果如下表(无废票):
语文 | 数学 | 外语 | 物理 | 化学 | 生物 | 政治 | 历史 | 地理 | |
高一(1)班 | 6 | 9 | 7 | 5 | 4 | 5 | 3 | 3 | 2 |
高一(7)班 |
| 6 |
| 4 | 5 | 6 | 5 | 2 | 3 |
该校把上表的数据作为样本,把两个班同一学科的得票之和定义为该年级该学科的“好感指数”.
(Ⅰ)如果数学学科的“好感指数”比高一年级其他文化课都高,求![]() 的所有取值;
的所有取值;
(Ⅱ)从高一(1)班投票给政治、历史、地理的学生中任意选取![]() 位同学,设随机变量
位同学,设随机变量![]() 为投票给地理学科的人数,求
为投票给地理学科的人数,求![]() 的分布列和期望;
的分布列和期望;
(Ⅲ)当![]() 为何值时,高一年级的语文、数学、外语三科的“好感指数”的方差最小?(结论不要求证明)
为何值时,高一年级的语文、数学、外语三科的“好感指数”的方差最小?(结论不要求证明)