题目内容
12.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点分别为F1,F2,O为坐标原点,A为右顶点,P为双曲线左支上一点,若$\frac{{{{|{P{F_2}}|}^2}}}{{|{P{F_1}}|-|{OA}|}}$存在最小值为12a,则双曲线一三象限的渐近线倾斜角的余弦值的最小值是( )| A. | $\frac{1}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{{2\sqrt{6}}}{5}$ | D. | $\frac{{\sqrt{3}}}{5}$ |
分析 设|PF1|-|OA|=m,则$\frac{{{{|{P{F_2}}|}^2}}}{{|{P{F_1}}|-|{OA}|}}$=$\frac{(3a+m)^{2}}{m}$=$m+\frac{9{a}^{2}}{m}$+6a≥12a,当且仅当m=3a,取等号,|PF1|=4a,可得5a≥c,$\frac{b}{a}$≤2$\sqrt{6}$,设双曲线一三象限的渐近线倾斜角为α,则0<tanα≤2$\sqrt{6}$,cosα≥$\frac{1}{5}$,即可得出结论.
解答 解:设|PF1|-|OA|=m,则$\frac{{{{|{P{F_2}}|}^2}}}{{|{P{F_1}}|-|{OA}|}}$=$\frac{(3a+m)^{2}}{m}$=$m+\frac{9{a}^{2}}{m}$+6a≥12a,
当且仅当m=3a,取等号,∴|PF1|=4a,
∴4a≥c-a,∴5a≥c,
∴25a2≥a2+b2,∴$\frac{b}{a}$≤2$\sqrt{6}$,
设双曲线一三象限的渐近线倾斜角为α,则0<tanα≤2$\sqrt{6}$,∴cosα≥$\frac{1}{5}$,
∴双曲线一三象限的渐近线倾斜角的余弦值的最小值是$\frac{1}{5}$,
故选:A.
点评 本题考查双曲线的方程与性质,考查基本不等式的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
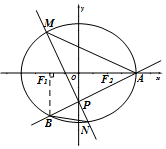 如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右顶点为A(2,0),左、右焦点分别为F1、F2,过点A且斜率为$\frac{1}{2}$的直线与y轴交于点P,与椭圆交于另一个点B,且点B在x轴上的射影恰好为点F1.
如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右顶点为A(2,0),左、右焦点分别为F1、F2,过点A且斜率为$\frac{1}{2}$的直线与y轴交于点P,与椭圆交于另一个点B,且点B在x轴上的射影恰好为点F1.