题目内容
a＞b＞0则a+
的最小值（ ）
| 1 |
| (a-b)b |
| A、1 | B、2 | C、3 | D、4 |
分析：本题可为三个数的和，将a+
变为a-b+b+
，用基本不等式求出最小值．
| 1 |
| (a-b)b |
| 1 |
| (a-b)b |
解答：解：∵a+
=a-b+b+
≥3
=3，
等号当且仅当a-b=b=
时成立'
故应选C．
| 1 |
| (a-b)b |
| 1 |
| (a-b)b |
| 3 | (a-b)×b×
| ||
等号当且仅当a-b=b=
| 1 |
| (a-b)b |
故应选C．
点评：本题考查三元的基本不等式公式，在人教A版本上是超纲内容．答题都答题时先确认自己学过相关公式否..
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
相关题目
”；
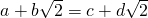?a=c，b=d”；③“若a，b∈R，则a-b＞0?a＞b”类比推出“若a，b∈C，则a-b＞0?a＞b”④“若x∈R，则|x|＜1?-1＜x＜1”类比推出“若z∈C，则|z|＜1?-1＜z＜1”．其中类比结论正确的命题是________．
⇒a=c，b=d”；③“若a，b∈R，则a-b＞0⇒a＞b”类比推出“若a，b∈C，则a-b＞0⇒a＞b”④“若x∈R，则|x|＜1⇒-1＜x＜1”类比推出“若z∈C，则|z|＜1⇒-1＜z＜1”．其中类比结论正确的命题是 ．