题目内容
相距480米有两个垂直于水平地面的高塔AB和CD，两塔底B，D的中点为P，已知AB=280米，CD=320米，则cos∠APC的值是 ．
分析：计算出△APC的三边，再利用余弦定理，可得结论．
解答：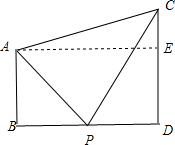
解：如图所示，AP=
=40
，CP=
=400，AC=
=40
．
在△APC中，cos∠APC=
=
=
．
故答案为：
．
解：如图所示，AP=| 2802+2402 |
| 85 |
| 3202+2402 |
| 4802+(320-280)2 |
| 145 |
在△APC中，cos∠APC=
| AP2+CP2-AC2 |
| 2AP•CP |
(40
| ||||
2•40
|
2
| ||
| 85 |
故答案为：
2
| ||
| 85 |
点评：本题考查余弦定理的运用，考查学生利用数学知识解决实际问题，正确运用余弦定理是关键．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
（示范高中）如图，在河的对岸可以看到两个目标物M，N，但不能到达，在河岸边选取相距40米的两个目标物P，Q两点，测得∠MPN=75°，∠NPQ=45°，∠MQP=30°，∠MQN=45°，试求两个目标物M，N之间的距离．
，
，
，
，试求两个目标物Ｍ，Ｎ之间的距离.
