Question

【题目】设是数列的前n项和，对任意都有，（其中k、b、p都是常数）.

（1）当、、时，求；

（2）当、、时，若、，求数列的通项公式；

（3）若数列中任意（不同）两项之和仍是该数列中的一项，则称该数列是“封闭数列”。当、、时，.试问：是否存在这样的“封闭数列”.使得对任意.都有，且.若存在，求数列的首项的所有取值的集合；若不存在，说明理由.

Answer 1

【答案】（1）；（2）；（3）.

【解析】

（1）得到，时化简得到，根据等比数列公式得到答案.

（2）根据题意化简得到，再代换得到，确定数列为等差数列，代入数据计算得到答案.

（3）根据（2）知数列为等差数列，取得到，根据封闭数列定义得到，得到，再排除的情况得到答案.

（1）当、、时，得到

当时，；

当时，，化简得到；

故

（2）当、、时，得到

当时，，两式相减化简得到；

代换得到，两式相减化简得到

故数列为等差数列：，，解得，

故

（3）当、、时，根据（2）知，数列为等差数列.

，即，

取时，，根据封闭数列定义得到

故

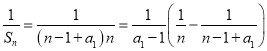
当时，，则

取得到，排除；

当时，，

则，满足；

当时，易知小于时对应的值，成立；

综上所述：