题目内容
椭圆的离心率为| 1 | 2 |
分析:由椭圆的离心率为
,知a=2c,设中心是(m,0),准线x=1,根据椭圆的第二定义可求.
| 1 |
| 2 |
解答:解:e=
,a=2c
设中心是(m,0),准线x=1,
因为椭圆中焦点比准线离中心更近,所以中心在(3,0)右边,所以m>3,则c=焦点到中心距离=m-3
准线到中心距离=
=m-1,所以
-c=2,所以
-c=2,∴c=
,∴a=
,b2=
,m=c+3=
所以椭圆3x2+4y2-22x+35=0,
故答案为:3x2+4y2-22x+35=0.
| 1 |
| 2 |
设中心是(m,0),准线x=1,
因为椭圆中焦点比准线离中心更近,所以中心在(3,0)右边,所以m>3,则c=焦点到中心距离=m-3
准线到中心距离=
| a2 |
| c |
| a2 |
| c |
| 4c2 |
| c |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 11 |
| 3 |
所以椭圆3x2+4y2-22x+35=0,
故答案为:3x2+4y2-22x+35=0.
点评:本题主要考查椭圆的第二定义,应注意椭圆的中心不在坐标原点,其方程不是标准方程,属于中档题

练习册系列答案
相关题目
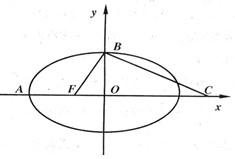 如图,F是椭圆
如图,F是椭圆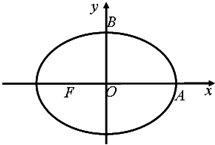 如图,点F是椭圆W:
如图,点F是椭圆W: