题目内容
【题目】已知![]() ,
,![]() ,
,![]() 分别为
分别为![]() 内角
内角![]() ,
,![]() ,
,![]() 的对边,若
的对边,若![]() 同时满足下列四个条件中的三个:①
同时满足下列四个条件中的三个:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
(1)满足有解三角形的序号组合有哪些?
(2)在(1)所有组合中任选一组,并求对应![]() 的面积.
的面积.
(若所选条件出现多种可能,则按计算的第一种可能计分)
【答案】(1)①,③,④或②,③,④;(2)![]() .
.
【解析】
(1)由①可求得![]() 的值,由②可求出角
的值,由②可求出角![]() 的值,结合题意得出
的值,结合题意得出![]() ,推出矛盾,可得出①②不能同时成为
,推出矛盾,可得出①②不能同时成为![]() 的条件,由此可得出结论;
的条件,由此可得出结论;
(2)在符合条件的两组三角形中利用余弦定理和正弦定理求出对应的边和角,然后利用三角形的面积公式可求出![]() 的面积.
的面积.
(1)由①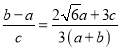 得,
得,![]() ,
,
所以![]() ,
,
由②![]() 得,
得,![]() ,
,
解得![]() 或
或![]() (舍),所以
(舍),所以![]() ,
,
因为![]() ,且
,且![]() ,所以
,所以![]() ,所以
,所以![]() ,矛盾.
,矛盾.
所以![]() 不能同时满足①,②.
不能同时满足①,②.
故![]() 满足①,③,④或②,③,④;
满足①,③,④或②,③,④;
(2)若![]() 满足①,③,④,
满足①,③,④,
因为![]() ,所以
,所以![]() ,即
,即![]() .
.
解得![]() .
.
所以![]() 的面积
的面积![]() .
.
若![]() 满足②,③,④由正弦定理
满足②,③,④由正弦定理![]() ,即
,即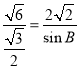 ,解得
,解得![]() ,
,
所以![]() ,所以
,所以![]() 的面积
的面积![]() .
.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目