题目内容
已知数列![]() 的相邻两项
的相邻两项![]() 是关于
是关于![]() 的方程
的方程![]() 的两实根,且
的两实根,且![]()
(Ⅰ)求证:数列![]() 是等比数列;
是等比数列;
(Ⅱ)![]() 是数列
是数列![]() 的前
的前![]() 项的和.问是否存在常数
项的和.问是否存在常数![]() ,使得
,使得![]() 对
对![]() 都成立,若存在,求出
都成立,若存在,求出![]() 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
解:(Ⅰ)证明:![]() 是关于
是关于![]() 的方程
的方程![]() 的两实根,
的两实根,
 ……2分
……2分

故数列![]() 是首项为
是首项为![]() ,公比为-1的等比数列.……4分
,公比为-1的等比数列.……4分
(Ⅱ)由(Ⅰ)得![]() ,即
,即![]()
![]()
![]() ……8分
……8分
因此,![]()
要使![]() ,对
,对![]() 都成立
都成立![]() ,
,
即![]() (*) ……10分
(*) ……10分
①当![]() 为正奇数时,由(*)式得:
为正奇数时,由(*)式得:![]()
即![]() ,
,
![]() 对任意正奇数
对任意正奇数![]() 都成立,
都成立,
因为![]() 为奇数)的最小值为1.所以
为奇数)的最小值为1.所以![]() ……12分
……12分
②当![]() 为正偶数时,由(*)式得:
为正偶数时,由(*)式得:
![]() , 即
, 即![]()
![]() 对任意正偶数
对任意正偶数![]() 都成立,因为
都成立,因为![]()
![]() 为偶数)的最小值为
为偶数)的最小值为![]()
![]()
所以,存在常数![]() ,使得
,使得![]() 对
对![]() 都成立时
都成立时![]() 的取值范围为
的取值范围为![]() .
.
……14分

练习册系列答案
相关题目
 的相邻两项
的相邻两项 是关于
是关于 的方程
的方程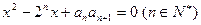 的两实根,且
的两实根,且 ,记数列
,记数列 项和为
项和为 .
. ;
; 是等比数列;
是等比数列; 设
设 ,问是否存在常数
,问是否存在常数 ,使得
,使得 对
对 都成立,若存在,
都成立,若存在, 的相邻两项
的相邻两项 是关于
是关于 的方程
的方程 的两根,且
的两根,且 .
. 是等比数列;
是等比数列; 项和
项和 ;
; 若
若 对任意的
对任意的 都成立,求
都成立,求 的取值范围。
的取值范围。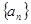 的相邻两项
的相邻两项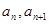 是关于
是关于 的方程
的方程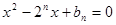
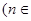 N
N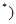 的两根,且
的两根,且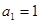 .
. 的通项公式;
的通项公式;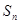 是数列
是数列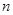 项和, 问是否存在常数
项和, 问是否存在常数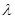 ,使得
,使得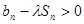 对任意
对任意 N
N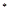 都成立,若存在, 求出
都成立,若存在, 求出 的相邻两项
的相邻两项 是关于
是关于 的方程
的方程 的两根,且
的两根,且
 是等比数列;
是等比数列; 项和
项和 ;
; 对任意的
对任意的 都成立,求
都成立,求 的取值范围。
的取值范围。 的相邻两项
的相邻两项 是关于
是关于 的方程
的方程 的两实根,且
的两实根,且 ,记数列
,记数列 项和为
项和为 .
. ;
; 是等比数列;
是等比数列; ,问是否存在常数
,问是否存在常数 ,使得
,使得 对
对 都成立,若存在,
都成立,若存在,