题目内容
如图所示,F1、F2分别为椭圆C: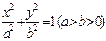 的左、右两个焦点,A、B为两个顶点,
的左、右两个焦点,A、B为两个顶点,
已知椭圆C上的点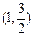 到F1、F2两点的距离之和为4.
到F1、F2两点的距离之和为4.
(Ⅰ)求椭圆C的方程和焦点坐标;
(Ⅱ)过椭圆C的焦点F2作AB的平行线交椭圆于P、Q两点,求△F1PQ的面积.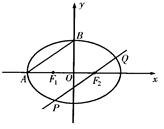
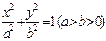 的左、右两个焦点,A、B为两个顶点,
的左、右两个焦点,A、B为两个顶点,已知椭圆C上的点
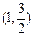 到F1、F2两点的距离之和为4.
到F1、F2两点的距离之和为4.(Ⅰ)求椭圆C的方程和焦点坐标;
(Ⅱ)过椭圆C的焦点F2作AB的平行线交椭圆于P、Q两点,求△F1PQ的面积.

(1)
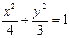 ,焦点F1、F2的坐标分别为(-1,0)和(1,0)
,焦点F1、F2的坐标分别为(-1,0)和(1,0)(2)
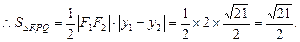
解:(Ⅰ)由题设知:2a = 4,即a = 2
将点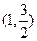 代入椭圆方程得
代入椭圆方程得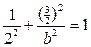 ,解得b2 = 3
,解得b2 = 3
∴c2 = a2-b2 = 4-3 =" 1 " ,故椭圆方程为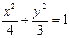 ,
,
焦点F1、F2的坐标分别为(-1,0)和(1,0)
(Ⅱ)由(Ⅰ)知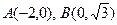 ,
,
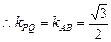 ,∴PQ所在直线方程为
,∴PQ所在直线方程为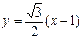 ,
,
由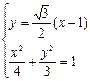 得
得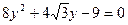
设P (x1,y1),Q (x2,y2),则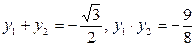 ,
,
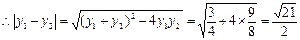
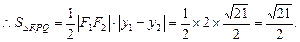
将点
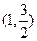 代入椭圆方程得
代入椭圆方程得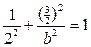 ,解得b2 = 3
,解得b2 = 3∴c2 = a2-b2 = 4-3 =" 1 " ,故椭圆方程为
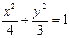 ,
,焦点F1、F2的坐标分别为(-1,0)和(1,0)
(Ⅱ)由(Ⅰ)知
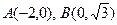 ,
,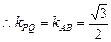 ,∴PQ所在直线方程为
,∴PQ所在直线方程为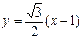 ,
,由
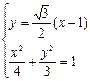 得
得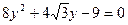
设P (x1,y1),Q (x2,y2),则
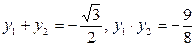 ,
,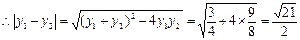

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
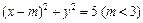 与椭圆E:
与椭圆E: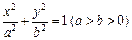
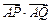 的取值范围.
的取值范围.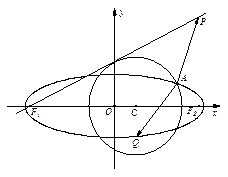 w.
w.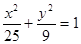 上一点M到焦点
上一点M到焦点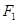 的距离为2,
的距离为2,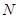 是
是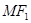 的中点,则
的中点,则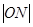 等于( )
等于( )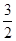
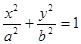 的两个焦点到一条准线的距离之比为3:2,则椭圆的离心率是( )
的两个焦点到一条准线的距离之比为3:2,则椭圆的离心率是( )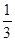 B
B 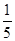 . C.
. C.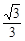 D
D 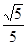
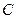 :
: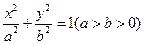 的长轴长是短轴长的
的长轴长是短轴长的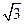 倍,
倍,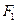 ,
,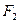 是左,右焦点.
是左,右焦点.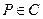 ,且
,且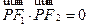 ,
,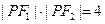 ,求
,求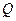 作以
作以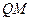 (
(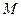 是切点),且使
是切点),且使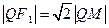 ,求动点
,求动点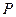 为椭圆
为椭圆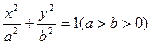 上一点,
上一点,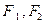 是椭圆的左、右焦点,若使△F1PF2为等边三角形,则椭圆离心率为 ▲ .
是椭圆的左、右焦点,若使△F1PF2为等边三角形,则椭圆离心率为 ▲ .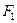 、
、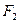 ,它们在第一象限
,它们在第一象限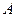 ,且
,且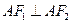 ,
,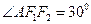 ,则椭圆与双曲
,则椭圆与双曲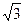

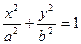 (a>b>0)的离心率
(a>b>0)的离心率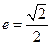 , 直线
, 直线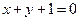 与椭圆交于P,Q两点, 且OP⊥OQ(如图) .
与椭圆交于P,Q两点, 且OP⊥OQ(如图) .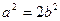 ;
;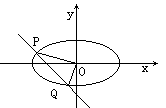
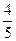 ,且过点
,且过点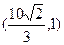 .
. 分别切椭圆C与圆
分别切椭圆C与圆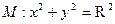 (其中3<R<5)于A、B两点,求|AB| 的最大值.
(其中3<R<5)于A、B两点,求|AB| 的最大值.