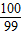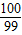题目内容
数列{an}的a1=1, =(n,an),
=(n,an),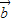 =(an+1,n+1),且
=(an+1,n+1),且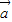 ⊥
⊥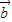 ,则a100=( )
,则a100=( )A.-100
B.100
C.
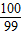
D.-
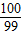
【答案】分析:根据题中已知条件先求出an与an+1的关系,再求出数列an的通项公式,将n=100代入an的通项公式即可求出a100的值.
解答:解:由题意 ⊥
⊥ ,
,
可知: ,
,
则有:a2=- a1,
a1,
a3=- a2,
a2,
a4=- a3,
a3,
a5=- a4,
a4,
…,
an-1=- an-2,
an-2,
 ,
,
∴an=(-1)n-1 ×
× ×
× ×
× ×…×
×…× ×
× a1=(-1)n-1 na1=(-1)n-1 n.
a1=(-1)n-1 na1=(-1)n-1 n.
∴a100=-100,
故选A.
点评:本题主要考查了数量积判断两个平面向量的垂直关系、由递推公式推导数列的通项公式,是高考的热点,考查了学生的计算能力和对数列的综合掌握,属于中档题.
解答:解:由题意
 ⊥
⊥ ,
,可知:
 ,
,则有:a2=-
 a1,
a1,a3=-
 a2,
a2,a4=-
 a3,
a3,a5=-
 a4,
a4,…,
an-1=-
 an-2,
an-2, ,
,∴an=(-1)n-1
 ×
× ×
× ×
× ×…×
×…× ×
× a1=(-1)n-1 na1=(-1)n-1 n.
a1=(-1)n-1 na1=(-1)n-1 n.∴a100=-100,
故选A.
点评:本题主要考查了数量积判断两个平面向量的垂直关系、由递推公式推导数列的通项公式,是高考的热点,考查了学生的计算能力和对数列的综合掌握,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 =(n,an),
=(n,an),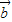 =(an+1,n+1),且
=(an+1,n+1),且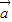 ⊥
⊥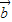 ,则a100=( )
,则a100=( )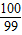
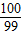
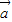 =(n,an),
=(n,an),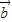 =(an+1,n+1),且
=(an+1,n+1),且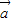 ⊥
⊥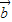 ,则a100=( )
,则a100=( )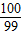
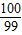
 =(n,an),
=(n,an),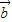 =(an+1,n+1),且
=(an+1,n+1),且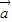 ⊥
⊥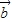 ,则a100=( )
,则a100=( )