题目内容
对于任何 与sinα+sinβ的大小关系是
与sinα+sinβ的大小关系是
- A.sin(α+β)<sinα+sinβ
- B.sin(α+β)>sinα+sinβ
- C.sin(α+β)=sinα+sinβ
- D.要以α,β的具体值而定
A
分析:利用两角和的正弦公式得到sin(α+β)=sinαcosβ+cosαsinβ,根据三角函数的有界性得到0<sinα<,0<cosβ<1,进一步得到sinαcosβ<sinα,同理osαsinβ<sinβ,利用不等式的可加性判断出sin(α+β)<sinα+sinβ,
解答:因为sin(α+β)=sinαcosβ+cosαsinβ,
又因为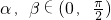
所以0<sinα<,0<cosβ<1,
所以sinαcosβ<sinα,
同理osαsinβ<sinβ,
所以sin(α+β)<sinα+sinβ,
故选A.
点评:本题考查两角和的正弦公式、三角函数的值域的求法以及不等式的性质,属于基础题.
分析:利用两角和的正弦公式得到sin(α+β)=sinαcosβ+cosαsinβ,根据三角函数的有界性得到0<sinα<,0<cosβ<1,进一步得到sinαcosβ<sinα,同理osαsinβ<sinβ,利用不等式的可加性判断出sin(α+β)<sinα+sinβ,
解答:因为sin(α+β)=sinαcosβ+cosαsinβ,
又因为
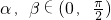
所以0<sinα<,0<cosβ<1,
所以sinαcosβ<sinα,
同理osαsinβ<sinβ,
所以sin(α+β)<sinα+sinβ,
故选A.
点评:本题考查两角和的正弦公式、三角函数的值域的求法以及不等式的性质,属于基础题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目