题目内容

对于任何α，β∈(0，
π
2
)，sin(α+β)与sinα+sinβ的大小关系是（　　）
A．sin（α+β）＜sinα+sinβB．sin（α+β）＞sinα+sinβ
C．sin（α+β）=sinα+sinβD．要以α，β的具体值而定
因为sin（α+β）=sinαcosβ+cosαsinβ，
又因为α，β∈(0，
π
2
)
所以0＜sinα＜，0＜cosβ＜1，
所以sinαcosβ＜sinα，
同理osαsinβ＜sinβ，
所以sin（α+β）＜sinα+sinβ，
故选A．
练习册系列答案
相关题目
f（x）是定义在D上的函数，若对任何实数α∈（0，1）以及D中的任意两数x1，x2，恒有f（αx1+（1-α）x2）≤αf（x1）+（1-α）f（x2），则称f（x）为定义在D上的C函数．
（Ⅰ）试判断函数f1（x）=x2，f2(x)=
1x
(x＜0)中哪些是各自定义域上的C函数，并说明理由；
（Ⅱ）已知f（x）是R上的C函数，m是给定的正整数，设an=f（n），n=0，1，2，…，m，且a0=0，am=2m，记Sf=a1+a2+…+am．对于满足条件的任意函数f（x），试求Sf的最大值；
（Ⅲ）若（Ⅱ）中Sf的最大值记为h（m），且h（1）+h（2）+…+h（m）≤a对任意给定的正整数m恒成立，试求a的取值范围．
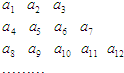精英家教网将数列{an}  中的所有项按第一排三项，以下每一行比上一行多一项的规则排成如数表：记表中的第一列数a1，a4，a8，…构成的数列为{bn}，已知：
①在数列{bn}  中，b1=1，对于任何n∈N*，都有（n+1）bn+1-nbn=0；
②表中每一行的数按从左到右的顺序均构成公比为q（q＞0）的等比数列；
③a66=
2
5
．请解答以下问题：
（1）求数列{bn}  的通项公式；
（2）求上表中第k（k∈N*）行所有项的和S（k）；
（3）若关于x的不等式S(k)+
1
k
＞
1-x2
x
在x∈[
1
1000
 ， 
1
100
]上有解，求正整数k的取值范围．
对于任何α，β∈(0，
π
2
)，sin(α+β)与sinα+sinβ的大小关系是（　　）

对于任何且xy≠0，则组成的集合所含的元素的个数是

[　　]

A．1
B．2
C．3
D．4

对于任何且xy≠0，则组成的集合所含的元素的个数是

[　　]

A．1
B．2
C．3
D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网