题目内容
已知角B为钝角的△ABC的内角A、B、C所对应边分别为a,b,c,若a=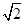 c,cosC=
c,cosC=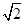 sinA,则cosB= ( )
sinA,则cosB= ( )
A. -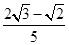
B. -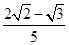
C. -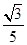
D. -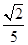
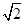 c,cosC=
c,cosC=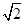 sinA,则cosB= ( )
sinA,则cosB= ( )A. -
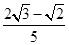
B. -
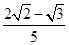
C. -
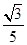
D. -
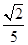
A
∵a=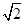 c,由正弦定理知,sinA=
c,由正弦定理知,sinA=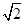 sinC
sinC
∴cosC=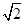 sinA=2sinC
sinA=2sinC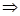 tanC=
tanC=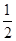
∵cos2C=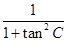 =
=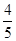 且角C为锐角
且角C为锐角
∴cosC=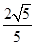
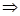 sinC=
sinC=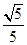 ,
,
sinA=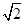 sinC =
sinC =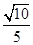
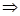 cosA=
cosA=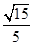
∵cosB=-cos(A+B)=-(cosAcosC-sinAsinC)
∴cosB=-(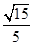 ×
×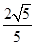 -
-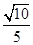 ×
×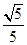 )=-
)=-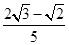
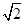 c,由正弦定理知,sinA=
c,由正弦定理知,sinA=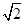 sinC
sinC∴cosC=
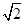 sinA=2sinC
sinA=2sinC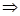 tanC=
tanC=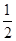
∵cos2C=
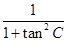 =
=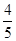 且角C为锐角
且角C为锐角∴cosC=
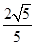
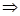 sinC=
sinC=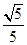 ,
,sinA=
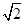 sinC =
sinC =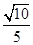
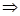 cosA=
cosA=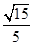
∵cosB=-cos(A+B)=-(cosAcosC-sinAsinC)
∴cosB=-(
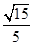 ×
×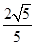 -
-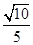 ×
×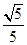 )=-
)=-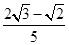

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
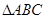 中,角
中,角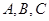 所对的边分别为
所对的边分别为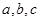 ,点
,点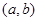 在直线
在直线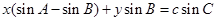 上.
上.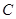 的值;
的值;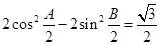 ,且
,且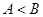 ,求
,求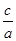 .
.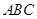 中,角
中,角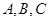 所对的边分别为
所对的边分别为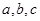 ,已知
,已知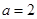 ,
,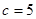 ,
,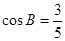 .
.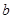 的值;
的值;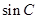 的值.
的值.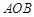 ,圆心角
,圆心角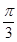 ,半径为2,在半径
,半径为2,在半径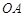 上有一动点
上有一动点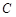 ,过点
,过点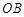 的直线交弧
的直线交弧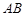 于点
于点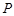 .
.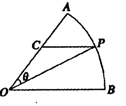
 的长;
的长;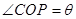 ,求
,求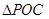 面积的最大值及此时
面积的最大值及此时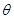 的值.
的值. 中,若
中,若 ,
, ,则
,则 的值为( )
的值为( )



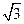 a+c,sinB-sinA),若m∥n,则角B的大小为( )
a+c,sinB-sinA),若m∥n,则角B的大小为( )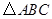 中,
中,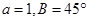 ,
,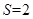 ,则
,则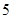
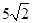
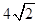
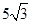
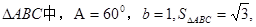 则
则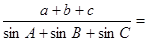 ( )
( )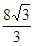
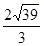
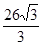
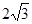
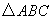 中,角
中,角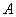 、
、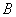 、
、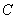 所对的边分别为
所对的边分别为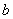 、
、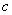 ,若
,若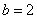 ,
,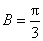 且
且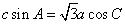 ,则
,则


