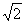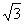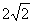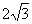题目内容
△ABC的三内角A,B,C所对边长分别是a,b,c,设向量m=(a+b,sinC),n=(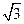 a+c,sinB-sinA),若m∥n,则角B的大小为( )
a+c,sinB-sinA),若m∥n,则角B的大小为( )
A.30°
B.60°
C.120°
D.150°
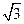 a+c,sinB-sinA),若m∥n,则角B的大小为( )
a+c,sinB-sinA),若m∥n,则角B的大小为( )A.30°
B.60°
C.120°
D.150°
D
∵m∥n,∴(a+b)(sinB-sinA)-sinC(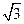 a+c)=0,由正弦定理有(a+b)(b-a)=c(
a+c)=0,由正弦定理有(a+b)(b-a)=c(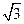 a+c),即a2+c2-b2=-
a+c),即a2+c2-b2=-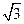 ac,再由余弦定理得cosB=-
ac,再由余弦定理得cosB=- ,∴B=150°.
,∴B=150°.
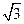 a+c)=0,由正弦定理有(a+b)(b-a)=c(
a+c)=0,由正弦定理有(a+b)(b-a)=c(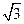 a+c),即a2+c2-b2=-
a+c),即a2+c2-b2=-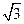 ac,再由余弦定理得cosB=-
ac,再由余弦定理得cosB=- ,∴B=150°.
,∴B=150°.
练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 ,相距10海里C处的乙船,乙船当即决定匀速前往救援,并且与甲船同时到达。(供参考使用:
,相距10海里C处的乙船,乙船当即决定匀速前往救援,并且与甲船同时到达。(供参考使用: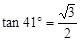 ).
).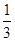 ,则sin∠BAC=________.
,则sin∠BAC=________. 则C=______________.
则C=______________.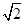 c,cosC=
c,cosC=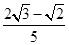
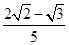
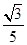
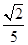
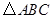 的面积
的面积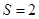 ,且
,且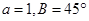 ,则
,则 ,则cosB的值为( )
,则cosB的值为( )



 ,且
,且 .若△ABC的面积为
.若△ABC的面积为 ,则角C的大小为( )
,则角C的大小为( )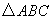 的三个内角A,B,C所对的边分别为
的三个内角A,B,C所对的边分别为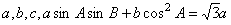 ,则
,则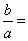 ( )
( )