题目内容
边长为2的菱形ABCD中，∠A=60°，沿BD折成直二面角，过点A作PA⊥平面ABD，且AP=2
．
（Ⅰ）求证：PA∥平面DBC；
（Ⅱ）求直线PC与平面DBC所成角的大小．
| 3 |
（Ⅰ）求证：PA∥平面DBC；
（Ⅱ）求直线PC与平面DBC所成角的大小．
（Ⅰ）取BD的中点O，连接CO，则
等边△BCD中，可得CO⊥BD． …（1分）
又∵平面DBC⊥平面ABD，平面DBC∩平面ABD=BD，
CO?平面DBC，CO⊥BD
∴CO⊥平面ABD． …（3分）
又∵AP⊥平面ABD，∴CO∥PA． …（4分）
∵CO?平面DBC，PA?平面DBC
∴PA∥平面DBC． …（7分）
（Ⅱ）∵CO∥PA，
∴O、A、P、C四点共面．
连接AO并延长交PC的延长线于H．
∵平面DBC⊥平面ABD，平面DBC∩平面ABD=BD，AH⊥BD，
∴AH⊥平面BCD，
∴直线CO即直线PH在平面BCD内的射影，可得∠HCO即直线PH平面BCD所成的角． …（10分）
∵CO∥PA且OC=
PA，可得OC是△PAH的中位线．
∴OH=OA=
．
又∵OC=
，可得Rt△HCO中，tan∠HCO=
=1
∴∠HCO=45°，即直线PC与平面DBC所成角为45°…（14分）
等边△BCD中，可得CO⊥BD． …（1分）
又∵平面DBC⊥平面ABD，平面DBC∩平面ABD=BD，
CO?平面DBC，CO⊥BD
∴CO⊥平面ABD． …（3分）
又∵AP⊥平面ABD，∴CO∥PA． …（4分）
∵CO?平面DBC，PA?平面DBC
∴PA∥平面DBC． …（7分）
（Ⅱ）∵CO∥PA，
∴O、A、P、C四点共面．
连接AO并延长交PC的延长线于H．
∵平面DBC⊥平面ABD，平面DBC∩平面ABD=BD，AH⊥BD，
∴AH⊥平面BCD，
∴直线CO即直线PH在平面BCD内的射影，可得∠HCO即直线PH平面BCD所成的角． …（10分）
∵CO∥PA且OC=
| 1 |
| 2 |
∴OH=OA=
| 3 |
又∵OC=
| 3 |
| HO |
| OC |
∴∠HCO=45°，即直线PC与平面DBC所成角为45°…（14分）
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
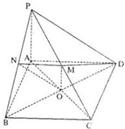如图，四棱锥P-ABCD的底面ABCD是边长为2的菱形，∠ABC=60°，点M是棱PC的中点，PA⊥平面ABCD，AC、BD交于点O．
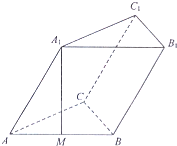已知斜三棱柱ABC-A1B1C1的底面是正三角形，侧面ABB1A1是边长为2的菱形，且∠A1AB=60°，M是AB的中点，MA1⊥AC．
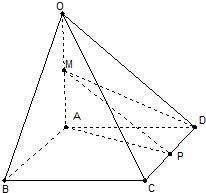如图，在四棱锥O-ABCD中，底面ABCD是边长为2的菱形，∠ABC=60°，OA⊥底面ABCD，OA=2，M为OA的中点，P为CD的中点．
（2013•渭南二模）如图，四棱锥P-ABCD中，底面ABCD是边长为2的菱形，Q是棱PA上的动点．
如图所示，四棱锥P-ABCD中，底面ABCD是边长为2的菱形，Q是PA的中点，BD⊥CQ，PA=PC，PB=3，∠ABC=60°．