题目内容
函数f（x）=sin（ωx+φ）•cos（ωx+φ）（ω＞0）以2为最小正周期，且能在x=2时取得最大值，则φ的一个值是
- A.
- B.
- C.
- D.
B
分析：先将f（x）化成一角一函数的形式，根据周期确定ω的值，再根据在x=2取得最大值确定φ的值．
解答：f（x）=sin（ωx+φ）•cos（ωx+φ）=
sin（2ωx+2φ），
∵T=2，故ω=
f（x）=sin（x+2φ），
当x=2时，×2+2φ=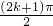
，
当k=-2时，φ=-
．
故选B．
点评：本题考查了由正弦函数的一些性质确定函数解析式，是基础题．
分析：先将f（x）化成一角一函数的形式，根据周期确定ω的值，再根据在x=2取得最大值确定φ的值．
解答：f（x）=sin（ωx+φ）•cos（ωx+φ）=
sin（2ωx+2φ），∵T=2，故ω=
f（x）=
sin（x+2φ），当x=2时，
×2+2φ=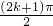，当k=-2时，φ=-
．故选B．
点评：本题考查了由正弦函数的一些性质确定函数解析式，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
函数f（x）=sin（ωx+?）（x∈R，ω＞0，0≤?＜2π）的部分图象如图，则