题目内容
曲线y=2x+sinx在点（π，2π）处的切线斜率为________．
1
分析：求出曲线方程的导函数，把切点的横坐标代入导函数求出的函数值即为切线方程的斜率．
解答：由y=2x+sinx，得到y′=2+cosx，
把x=π代入得：y′|x=π=2-1=1．
则曲线在点（π，2π）处的切线斜率为1．
故答案为：1
点评：此题考查学生会利用导数求曲线上过某点切线方程的斜率，是一道基础题．
分析：求出曲线方程的导函数，把切点的横坐标代入导函数求出的函数值即为切线方程的斜率．
解答：由y=2x+sinx，得到y′=2+cosx，
把x=π代入得：y′|x=π=2-1=1．
则曲线在点（π，2π）处的切线斜率为1．
故答案为：1
点评：此题考查学生会利用导数求曲线上过某点切线方程的斜率，是一道基础题．
练习册系列答案
相关题目
[选做题]在A、B、C、D四小题中只能选做2题，每小题10分，计20分．请把答案写在答题纸的指定区域内．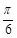
)的图像可由曲线y＝1＋cos2x向左平移
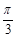个单位得到；②函数y＝sin(x＋
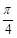)＋cos(x＋
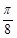是曲线y＝sin(2x＋
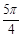)的一条对称轴；④函数y＝2sin2(x＋