题目内容
(本题满分12分)
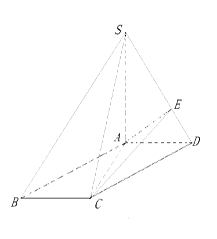
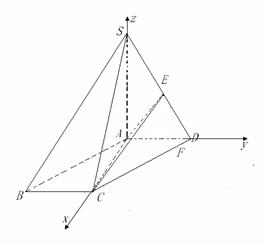
如图,在四棱锥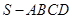 中,底面
中,底面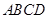 为平行四边形,
为平行四边形,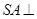 平面
平面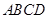 ,
,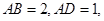
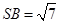
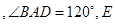 在棱
在棱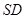 上.
上.
(I)当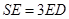 时,求证
时,求证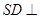 平面
平面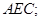
(II)当二面角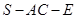 的大小为
的大小为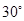 时,求直线
时,求直线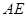 与平面
与平面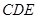 所成角的正弦值.
所成角的正弦值.
如图,在四棱锥
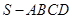 中,底面
中,底面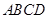 为平行四边形,
为平行四边形,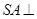 平面
平面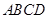 ,
,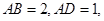
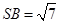
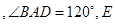 在棱
在棱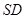 上.
上.
(I)当
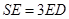 时,求证
时,求证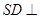 平面
平面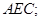
(II)当二面角
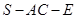 的大小为
的大小为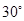 时,求直线
时,求直线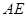 与平面
与平面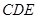 所成角的正弦值.
所成角的正弦值.(I)见解析(II)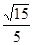
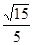
试题分析:(Ⅰ)在平行四边形
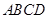 中,
中,由
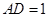 ,
,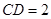 ,
,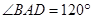 ,
,易知
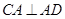 , ……2分
, ……2分又
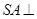 平面
平面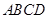 ,所以
,所以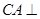 平面
平面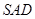 ,∴
,∴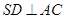 ,
,在直角三角形
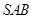 中,易得
中,易得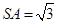 ,
,在直角三角形
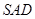 中,
中,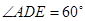 ,
,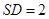 ,又
,又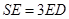 ,∴
,∴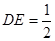 ,
,可得
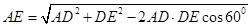
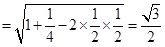 .
.∴
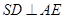 , ……5分
, ……5分又∵
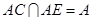 ,∴
,∴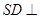 平面
平面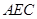 . ……6分
. ……6分(Ⅱ)由(Ⅰ)可知,
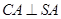 ,
,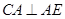 ,
,可知
 为二面角
为二面角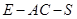 的平面角,
的平面角, 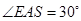 ,此时
,此时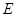 为
为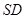 的中点. ……8分
的中点. ……8分过
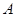 作
作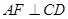 ,连结
,连结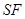 ,则平面
,则平面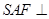 平面
平面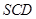 ,
,作
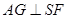 ,则
,则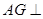 平面
平面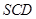 ,连结
,连结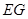 ,
,可得
 为直线
为直线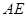 与平面
与平面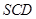 所成的角.
所成的角.因为
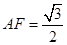 ,
,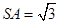 ,
,所以
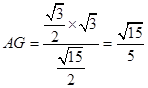 . ……10分
. ……10分在
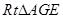 中,
中,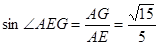 ,
,直线
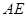 与平面
与平面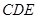 所成角的正弦值为
所成角的正弦值为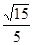 . ……12分
. ……12分解法二:依题意易知
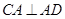 ,
,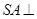 平面ACD.以A为坐标原点,AC、AD、SA分别为
平面ACD.以A为坐标原点,AC、AD、SA分别为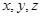 轴建立空间直角坐标系,则易得
轴建立空间直角坐标系,则易得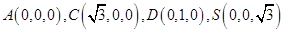 ,
,
(Ⅰ)由
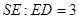 有
有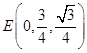 , ……3分
, ……3分易得
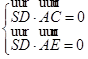 ,从而
,从而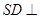 平面
平面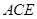 . ……6分
. ……6分(Ⅱ)由
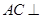 平面
平面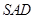 ,二面角
,二面角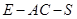 的平面角
的平面角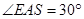 .
.又
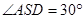 ,则
,则 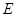 为
为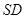 的中点,
的中点, 即
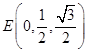 , ……8分
, ……8分设平面
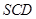 的法向量为
的法向量为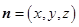
则
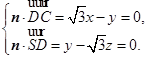 ,令
,令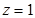 ,得
,得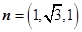 , ……10分
, ……10分从而
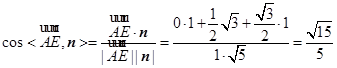 ,
,直线
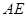 与平面
与平面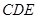 所成角的正弦值为
所成角的正弦值为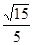 . ……12分
. ……12分点评:解决空间立体几何问题可以用传统的方法证明也可以用向量方法来证明,用传统方法证明时,要把证明所用的定理的条件摆清楚,缺一不可,用向量方法时,运算量比较大.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
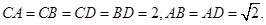
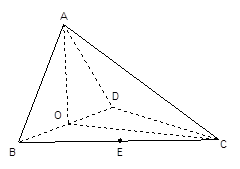
 平面BCD;
平面BCD;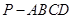 中,底面
中,底面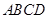 是矩形,
是矩形,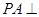 平面
平面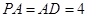 ,
,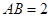 ,点
,点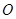 为
为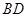 的中点,
的中点,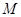 为
为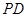 中点.
中点.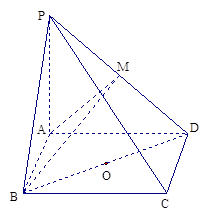
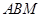 ⊥平面
⊥平面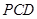 ;
;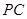 与平面
与平面 与
与 均为菱形,
均为菱形,  ,且
,且 ,
,
 平面
平面 ;
; 的余弦值。
的余弦值。 是直线,
是直线, ,
, 是两个不同的平面,下列选项正确的是( )
是两个不同的平面,下列选项正确的是( ) ⊥
⊥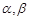 为两个不重合的平面,
为两个不重合的平面,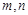 为两条不重合的直线,
为两条不重合的直线,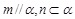 ,则
,则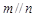 ;
;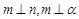 ,则
,则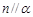 ;
; 则
则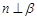 ;
;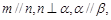 则
则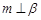 .
.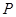 在正方体
在正方体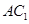 的对角线
的对角线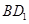 上.过点
上.过点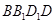 的直线,与正方体表面相交于
的直线,与正方体表面相交于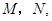 设
设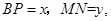 则函数
则函数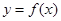 的图象大致是( )
的图象大致是( )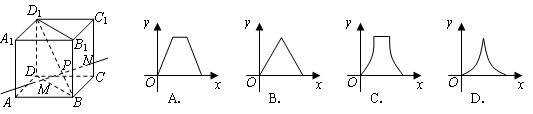
 中,下列几种说法正确的是 ( )
中,下列几种说法正确的是 ( )

 与
与 成
成 角
角 与
与 成
成 角
角
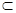 α,则α∥β;
α,则α∥β;