题目内容
抛物线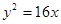 的准线经过双曲线
的准线经过双曲线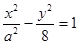 的一个焦点,则双曲线的离心率为
的一个焦点,则双曲线的离心率为
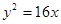 的准线经过双曲线
的准线经过双曲线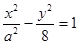 的一个焦点,则双曲线的离心率为
的一个焦点,则双曲线的离心率为 
分析:抛物线y2=16x的准线为 x=-4,故有 16=a2+8,求得a 值,即得 c/a=
 /a的值。
/a的值。解答:
抛物线y2=16x的准线为 x=-4,故有 16=a2+8,
∴a=2
 ,
,∴c/a=
 /a=
/a= 。
。点评:本题考查抛物线的标准方程,以及简单性质,双曲线的标准方程,以及双曲线的简单性质的应用,得到16=a2+8,求出 a值,是解题的关键。

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
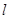 ,使得
,使得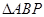 的面积最大时点P的坐标.
的面积最大时点P的坐标.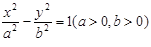 的左、右支分别交于M、N两点,与双曲线C的右准线相交于P点,F为右焦点,若|FM|=2|FN|,又
的左、右支分别交于M、N两点,与双曲线C的右准线相交于P点,F为右焦点,若|FM|=2|FN|,又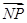 =λ
=λ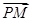 (λ∈R),则实数λ的值为( )
(λ∈R),则实数λ的值为( )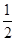
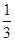
 ,当
,当 时,该曲线的离心率
时,该曲线的离心率 的取值范围是( )
的取值范围是( )



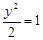 的右焦点作直线交双曲线于A、B两点,且
的右焦点作直线交双曲线于A、B两点,且 ,则这样的直线有___________条
,则这样的直线有___________条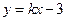 与双曲线
与双曲线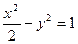 有且只有一个公共点,但直线与双曲线不相切,则实数
有且只有一个公共点,但直线与双曲线不相切,则实数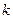 的值是
的值是  -
- =1的左焦点在抛物线y2=2px的准线上,则p的值为______
=1的左焦点在抛物线y2=2px的准线上,则p的值为______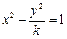 的焦点到渐近线的距离为
的焦点到渐近线的距离为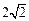 ,则实数k的值是
,则实数k的值是  的距离之和为4,则曲线C的方程是
的距离之和为4,则曲线C的方程是