题目内容
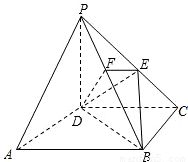 如图ABCD为正方形,PD⊥平面AC,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
如图ABCD为正方形,PD⊥平面AC,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.(1)证明:PA∥平面EDB;
(2)证明:PB⊥平面EFD.
【答案】分析:(1)连接AC,设AC∩BD=0,连接EO,底面是正方形,可得OE为△PAC的中位线,再利用直线与平面平行的判定定理进行证明,即可解决问题;
(2)PD⊥平面AC,BC?平面AC,所以BC⊥PD,而BC⊥CD,PD∩CD=D,可得BC⊥平面PDC在△PDC为等腰三角形中证明DE⊥平面PBC,从而求证.
解答:解:(1)连接AC,设AC∩BD=0,连接EO,
∵底面是正方形,
∴O为AC的中点
∴OE为△PAC的中位线
∴PA∥OE,而OE?平面EDB,PA∉平面EBD,
∴PA∥平面EDB.
(2)∵PD⊥平面AC,BC?平面AC,
∴BC⊥PD,而BC⊥CD,PD∩CD=D.
∴BC⊥平面PDC.
∵DE?平面PDC,
∴BC⊥DE.①
又∵PD⊥平面AC,DC?平面AC,
∴PD⊥DC,而PD=DC,
∴△PDC为等腰三角形.∴DE⊥PC.②
由①、②可知DE⊥平面PBC,
∴DE⊥PB.又EF⊥PB,
∴PB⊥平面DEF.
点评:此题考查直线与平面平行的判断及直线与平面垂直的判断,此类问题一般先证明两个面平行,再证直线和面平行,这种做题思想要记住,此类立体几何题是每年高考必考的一道大题,同学们要课下要多练习.
(2)PD⊥平面AC,BC?平面AC,所以BC⊥PD,而BC⊥CD,PD∩CD=D,可得BC⊥平面PDC在△PDC为等腰三角形中证明DE⊥平面PBC,从而求证.
解答:解:(1)连接AC,设AC∩BD=0,连接EO,
∵底面是正方形,
∴O为AC的中点
∴OE为△PAC的中位线
∴PA∥OE,而OE?平面EDB,PA∉平面EBD,
∴PA∥平面EDB.
(2)∵PD⊥平面AC,BC?平面AC,
∴BC⊥PD,而BC⊥CD,PD∩CD=D.
∴BC⊥平面PDC.
∵DE?平面PDC,
∴BC⊥DE.①
又∵PD⊥平面AC,DC?平面AC,
∴PD⊥DC,而PD=DC,
∴△PDC为等腰三角形.∴DE⊥PC.②
由①、②可知DE⊥平面PBC,
∴DE⊥PB.又EF⊥PB,
∴PB⊥平面DEF.
点评:此题考查直线与平面平行的判断及直线与平面垂直的判断,此类问题一般先证明两个面平行,再证直线和面平行,这种做题思想要记住,此类立体几何题是每年高考必考的一道大题,同学们要课下要多练习.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
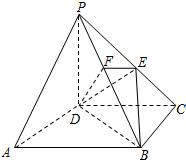 16、如图ABCD为正方形,PD⊥平面AC,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
16、如图ABCD为正方形,PD⊥平面AC,PD=DC,E是PC的中点,作EF⊥PB交PB于点F. (2006•南汇区二模)如图ABCD为正方形,EF∥AB,且DE:EA=3:4,EF交AC于Q,沿EF将正方形折成直二面角,
(2006•南汇区二模)如图ABCD为正方形,EF∥AB,且DE:EA=3:4,EF交AC于Q,沿EF将正方形折成直二面角,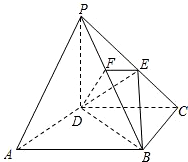
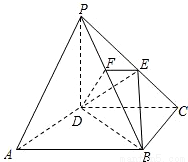 如图ABCD为正方形,PD⊥平面AC,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
如图ABCD为正方形,PD⊥平面AC,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.