题目内容
(本小题满分13分)
已知 是定义在[-1,1]上的奇函数,且
是定义在[-1,1]上的奇函数,且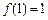 ,若任意的
,若任意的 ,当
,当 时,总有
时,总有 .
.
(1)判断函数 在[-1,1]上的单调性,并证明你的结论;
在[-1,1]上的单调性,并证明你的结论;
(2)解不等式: ;
;
(3)若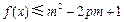 对所有的
对所有的 恒成立,其中
恒成立,其中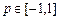 (
(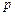 是常数),试用常数
是常数),试用常数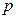 表示实数
表示实数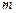 的取值范围.
的取值范围.
已知
 是定义在[-1,1]上的奇函数,且
是定义在[-1,1]上的奇函数,且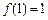 ,若任意的
,若任意的 ,当
,当 时,总有
时,总有 .
.(1)判断函数
 在[-1,1]上的单调性,并证明你的结论;
在[-1,1]上的单调性,并证明你的结论;(2)解不等式:
 ;
;(3)若
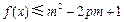 对所有的
对所有的 恒成立,其中
恒成立,其中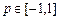 (
(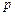 是常数),试用常数
是常数),试用常数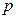 表示实数
表示实数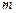 的取值范围.
的取值范围.(1) 在
在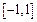 上是增函数,证明如下:
上是增函数,证明如下:
任取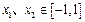 ,且
,且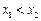 ,则
,则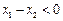 ,于是有
,于是有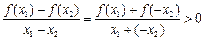 ,而
,而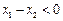 ,故
,故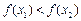 ,故
,故 在
在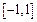 上是增函数
上是增函数
(2)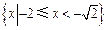 .
.
(3)由(1)知 最大值为
最大值为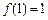 ,所以要使
,所以要使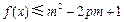 对所有的
对所有的 恒成立,只需
恒成立,只需 成立,即
成立,即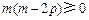 成立.
成立.
①当 时,
时,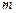 的取值范围为
的取值范围为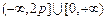 ;
;
②当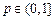 时,
时,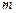 的取值范围为
的取值范围为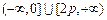 ;
;
③当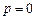 时,
时,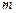 的取值范围为R.
的取值范围为R.
 在
在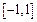 上是增函数,证明如下:
上是增函数,证明如下:任取
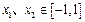 ,且
,且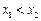 ,则
,则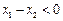 ,于是有
,于是有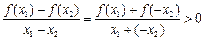 ,而
,而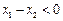 ,故
,故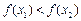 ,故
,故 在
在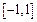 上是增函数
上是增函数(2)
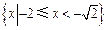 .
.(3)由(1)知
 最大值为
最大值为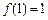 ,所以要使
,所以要使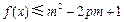 对所有的
对所有的 恒成立,只需
恒成立,只需 成立,即
成立,即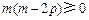 成立.
成立.①当
 时,
时,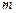 的取值范围为
的取值范围为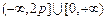 ;
;②当
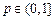 时,
时,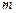 的取值范围为
的取值范围为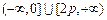 ;
;③当
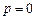 时,
时,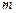 的取值范围为R.
的取值范围为R.(1) 在
在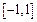 上是增函数,证明如下:
上是增函数,证明如下:
任取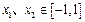 ,且
,且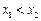 ,则
,则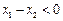 ,于是有
,于是有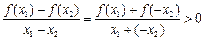 ,而
,而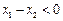 ,故
,故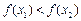 ,故
,故 在
在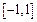 上是增函数
上是增函数
(2)由 在
在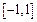 上是增函数知:
上是增函数知:
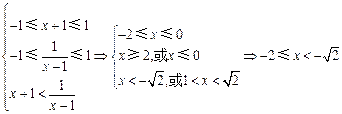 ,
,
故不等式的解集为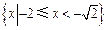 .
.
(3)由(1)知 最大值为
最大值为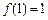 ,所以要使
,所以要使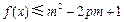 对所有的
对所有的 恒成立,只需
恒成立,只需 成立,即
成立,即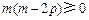 成立.
成立.
①当 时,
时,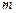 的取值范围为
的取值范围为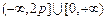 ;
;
②当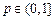 时,
时,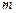 的取值范围为
的取值范围为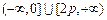 ;
;
③当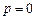 时,
时,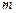 的取值范围为R.
的取值范围为R.
 在
在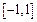 上是增函数,证明如下:
上是增函数,证明如下:任取
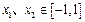 ,且
,且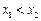 ,则
,则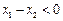 ,于是有
,于是有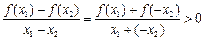 ,而
,而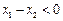 ,故
,故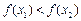 ,故
,故 在
在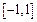 上是增函数
上是增函数(2)由
 在
在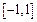 上是增函数知:
上是增函数知: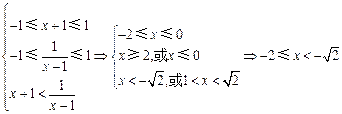 ,
,故不等式的解集为
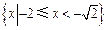 .
.(3)由(1)知
 最大值为
最大值为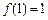 ,所以要使
,所以要使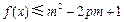 对所有的
对所有的 恒成立,只需
恒成立,只需 成立,即
成立,即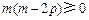 成立.
成立.①当
 时,
时,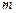 的取值范围为
的取值范围为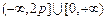 ;
;②当
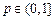 时,
时,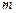 的取值范围为
的取值范围为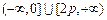 ;
;③当
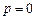 时,
时,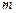 的取值范围为R.
的取值范围为R.
练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
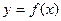 对任意
对任意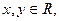 恒有
恒有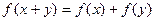 .
.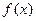 在其定义域上单调递减,对任意实数
在其定义域上单调递减,对任意实数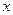 ,恒有
,恒有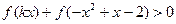 成立,求
成立,求 的取值范围.
的取值范围. 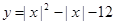 两个零点的差的绝对值是( ).
两个零点的差的绝对值是( ).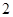

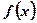 是
是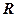 上的增函数,
上的增函数,
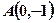 ,
,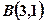 是其图像上的两点,那么
是其图像上的两点,那么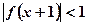 的解集的补集是( )
的解集的补集是( )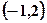
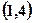
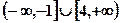
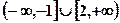
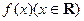 为奇函数,
为奇函数,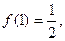
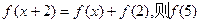 =" " ( )
=" " ( )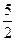
 ,
, ,且
,且 满足
满足 ,若
,若 的最大值和最小值分别为M、N,则M+N=( )
的最大值和最小值分别为M、N,则M+N=( )
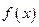 是偶函数,并且对于定义域内任意的
是偶函数,并且对于定义域内任意的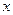 ,满足
,满足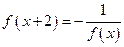 ,
,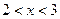 时,
时,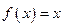 ,则
,则 =__________ ______.
=__________ ______. 是奇函数,它们的定域
是奇函数,它们的定域 ,且它们在
,且它们在 上的图象如图所示,则不等式
上的图象如图所示,则不等式 的解集是 .
的解集是 .
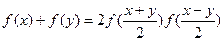 ,且f(0)≠0,那么f(x) ( )
,且f(0)≠0,那么f(x) ( )