题目内容

在直线x-y+2=0上求一点，使它到直线3x-4y+8=0、3x-y-1=00的距离平方和最小．
设直线x-y+2=0上的一点（x0，y0）到两直线的距离分别为d1和d2，
∵d1=
|3x0-4y0+8|
5
=
|-x0|
5
，d2=
|3x0-y0-1|
10
=
|2x0-3|
10
，
设S=d12+d22，
∴S=
x20
25
+
4
x20
-12x0+9
10
=
22
50
[(x0-
15
11
)2+
45
242
]
∴x0=
15
11
时，S有最小值．
这时，y0=x0+2=
37
11
，
而所求的点为(
15
11
，
37
11
)．
练习册系列答案
相关题目
在极坐标系中，点P(2，
11π
6
)到直线ρsin(θ-
π
6
)=1的距离等于______．
如图，已知长方形ABCD的两条对角线的交点为E（1，0），且AB与BC所在的直线方程分别为：x+3y-5=0与ax-y+5=0．
（1）求a的值；
（2）求DA所在的直线方程．
己知直线l1：x+y+1=0，l2：x+y-1=0，则l1，l2之间的距离为______．
直线l1过点A（0，1），l2过点B（5，0），如果l1∥l2，且l1与l2的距离为5，求l1、l2的方程．
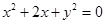以圆的圆心为圆心，半径为2的圆的方程
A．B．
C．D．
已知圆：，圆：，过圆上任意一点作圆的两条切线、，切点分别为、，则的最小值是（ ）
A．5B．6C．10D．12
点P（2，3）到直线：x+y+3=0的距离为d，则d的值为（　　）
A．1B．2
2
C．4
2
D．4
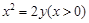圆心在抛物线上，并且与抛物线的准线及y轴均相切的圆的方程是（   ）
A．B．
C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网