题目内容
在等腰梯形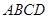 中,
中,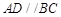 ,
,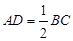 ,
,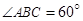 ,
,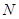 是
是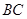 的中点.将梯形
的中点.将梯形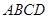 绕
绕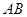 旋转
旋转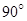 ,得到梯形
,得到梯形 (如图).
(如图).

(1)求证: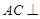 平面
平面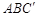 ;
;
(2)求证: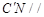 平面
平面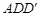 ;
;
(3)求二面角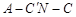 的余弦值.
的余弦值.
【答案】
(1)根据题意,由于即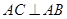 由已知可知 平面
由已知可知 平面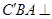 平面
平面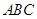 ,结合面面垂直的性质定理得到.
,结合面面垂直的性质定理得到.
(2)结合题意,得到面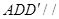 平面
平面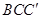 ,又因为
,又因为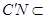 平面
平面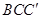 ,所以
,所以
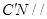 平面
平面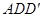 从而得到证明.
从而得到证明.
(3) 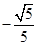
【解析】
试题分析:(1)证明:因为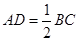 ,
,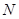 是
是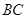 的中点
的中点
所以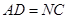 ,又
,又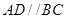
所以四边形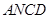 是平行四边形,所以
是平行四边形,所以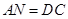
又因为等腰梯形,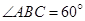 ,
,
所以 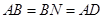 ,所以四边形
,所以四边形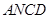 是菱形,所以
是菱形,所以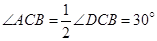

所以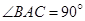 ,即
,即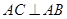
由已知可知 平面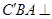 平面
平面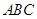 ,
,
因为 平面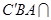 平面
平面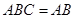
所以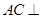 平面
平面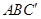 4分
4分
(2)证明:因为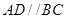 ,
,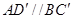 ,
,
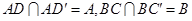
所以平面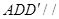 平面
平面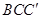
又因为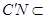 平面
平面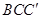 ,所以
,所以
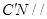 平面
平面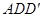 8分
8分
(3)因为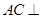 平面
平面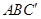 ,同理
,同理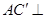 平面
平面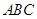 ,建立如图如示坐标系
,建立如图如示坐标系
设 ,
,
则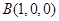 ,
,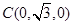 ,
, 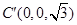 ,
,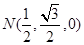 ,
9分
,
9分
则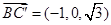 ,
,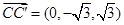
设平面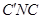 的法向量为
的法向量为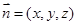 ,有
,有 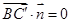 ,
,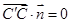 得
得 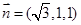
设平面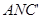 的法向量为
的法向量为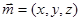 ,有
,有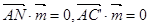
得
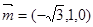 12分
12分
所以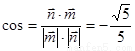 13分
13分
由图形可知二面角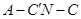 为钝角
为钝角
所以二面角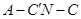 的余弦值为
的余弦值为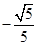 .
14分
.
14分
考点:平行和垂直的证明以及二面角的平面角
点评:主要是考查了线面平行以及面面平行的性质定理的运用,以及二面角的求解,属于基础题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
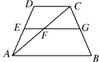 如图,在等腰梯形中,AB∥CD,AD=12 cm,AC交梯形中位线EG于点F,EF=4cm,
如图,在等腰梯形中,AB∥CD,AD=12 cm,AC交梯形中位线EG于点F,EF=4cm, 中,
中, ,
, ,
, 为
为 中点.将
中点.将 沿
沿 折起至
折起至 ,使得平面
,使得平面 平面
平面 ,
, 分别为
分别为 的中点.
的中点. 面
面 ;
; 的余弦值.
的余弦值. 中,
中, ,且
,且 。设以
。设以 为焦点且过点
为焦点且过点 的双曲线的离心率为
的双曲线的离心率为 ,以
,以 为焦点且过点
为焦点且过点 的椭圆的离心率为
的椭圆的离心率为 ,则
,则 = ;
= ; 中,
中, ,且
,且 .设
.设 ,以
,以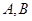 为焦点且过点
为焦点且过点 的双曲线的离心率为
的双曲线的离心率为 ,以
,以 为焦点且过点
为焦点且过点 的椭圆的离心率为
的椭圆的离心率为 ,则
( )
,则
( )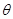 的增大,
的增大, 为定值
为定值