题目内容
已知函数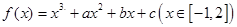 ,且函数
,且函数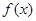 在
在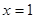 和
和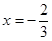 处都取得极值。
处都取得极值。
(1)求实数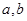 的值;
的值;
(2)求函数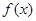 的极值;
的极值;
(3)若对任意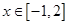 ,
,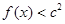 恒成立,求实数
恒成立,求实数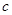 的取值范围。
的取值范围。
【答案】
(1) ;(2)
;(2) 或
或 。
。
【解析】本试题主要是考查了导数在研究函数中的运用。
(1)
由题意可知 ,解得
,解得
得到解析式。
(2)由(1)知 然后分析导数的符号与函数单调性的关系得到极值。
然后分析导数的符号与函数单调性的关系得到极值。
(3)对任意 ,
, 恒成立,,那么只要求解函数f(x)的最大值即可。
恒成立,,那么只要求解函数f(x)的最大值即可。
解:(1)
由题意可知 ,解得
,解得
(2)由(1)知 ,
,
|
|
|
|
|
1 |
|
|
|
|
极大值 |
- |
极小值 |
+ |
|
|
|
|
|
|
|

 时,
时, 的最大值为
的最大值为
 对于任意的
对于任意的 ,
, 恒成立,
恒成立,
 只需
只需 ,
, 或
或 。
。

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目






 +
+



 ,
,
 且函数
且函数 的最小正周期为
的最小正周期为 .
.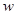 的值和函数
的值和函数 中,角A、B、C所对的边分别是
中,角A、B、C所对的边分别是 、
、 、
、 ,又
,又 ,
, ,
,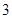 ,求边长
,求边长