题目内容
已知函数
，
且函数
的最小正周期为
.
(1)求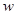
的值和函数的单调增区间；
(2)在
中，角A、B、C所对的边分别是
、
、
，又
，
，的面积等于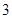
，求边长的值．
【答案】
(1) 单调增区间为
；（2）
.
【解析】
试题分析：(1)先将
化为一角一函数形式为
，再根据最小正周期为
求出
，然后根据正弦函数的性质求单调增区间.(2) 由
得
，然后根据面积公式
得出
，再由余弦定理解得
.
试题解析：（1）因为
2分
由的最小正周期为，得 
3分
即
5分
所以，函数的增区间为
6分
（2）
8分
10分
由余弦定理
12分
考点：1.三角函数；2.三角形面积公式；3.余弦定理.
练习册系列答案
相关题目
，
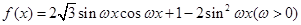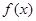的最小正周期为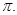
，求函数
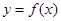的图象上各点的纵坐标保持不变，横坐标缩短到原来的
，把所得到的图象再向左平移
个单位，得到函数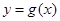
的图象，求函数
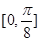上的最小值。
，且函数
的最小正周期
，求函数
的图象上各点的纵坐标保持不变，横坐标缩短到原来的
，把所得到的图象再向左平移
个单位，得到函数
的图象，求函数
上的最小值。
，且函数
的最小正周期为
，求函数
的图象上各点的纵坐标保持不变，横坐标缩短到原来的
，把所得到的图象再向左平移
个单位，得到函数
的图象，求函数
上的最小值。