题目内容
设长方体的长,宽,高分别是 ,其顶点都在一个球面上,则该球的表面积为( )
,其顶点都在一个球面上,则该球的表面积为( )
A. | B. | C. | D. |
D
解析试题分析:本题考查的知识点是球的体积和表面积公式,由长方体的长、宽、高分别为2a、a、a,其顶点都在一个球面上,则长方体的对角线即为球的直径,即球的半径R满足(2R)2=6a2,代入球的表面积公式,S球=4πR2,即可得到答案.解:根据题意球的半径R满足(2R)2=6a2,所以S球=4πR2=6πa2.故选D
考点:长方体的外接球
点评:主要是考查了长方体的外接球直径等于长方体的对角线长.

练习册系列答案
相关题目
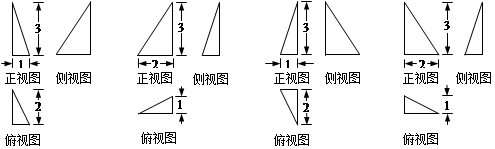
如图⑴、⑵、⑶、⑷为四个几何体的三视图,根据三视图可以判断这四个几何体依次分别为
| A.三棱台、三棱柱、圆锥、圆台 | B.三棱台、三棱锥、圆锥、圆台 |
| C.三棱柱、正四棱锥、圆锥、圆台 | D.三棱柱、三棱台、圆锥、圆台 |
棱长都是1的三棱锥的表面积为( )
A. | B.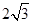 | C.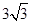 | D. |
已知正三棱柱底面边长是2,,外接球的表面积是 ,则该三棱柱的侧棱长( ).
,则该三棱柱的侧棱长( ).
A. | B. | C. | D. |










 长为2;侧视图一直角三角形;俯视图为一直角梯形,且
长为2;侧视图一直角三角形;俯视图为一直角梯形,且 ,则此几何体的体积是( )。
,则此几何体的体积是( )。