题目内容
某校高三(1)班共有40名学生,他们每天自主学习的时间全部在180分钟到330分钟之间,按他们学习时间的长短分5个组统计得到如下频率分布表:| 分组 | 频数 | 频率 |
| [180,210) | 4 | 0.1 |
| [210,240) | 8 | s |
| [240,270) | 12 | 0.3 |
| [270,300) | 10 | 0.25 |
| [300,330) | n | t |
(2)某兴趣小组为研究每天自主学习的时间与学习成绩的相关性,需要在这40名学生中按时间用分层抽样的方法抽取20名学生进行研究,问应抽取多少名第一组的学生?
(3)已知第一组的学生中男、女生均为2人.在(2)的条件下抽取第一组的学生,求既有男生又有女生被抽中的概率.
分析:(1)根据频率,频数和样本容量之间的关系得到s的值,根据频率分布表中的所有的频率之和是1得到t的值.
(2)在这40名学生中按时间用分层抽样的方法抽取20名学生进行研究,得到每个个体被抽到的概率,根据概率相等写出比例式,得到要求的第二组要抽取的人数.
(3)本题是一个古典概型,试验发生事件是按时间用分层抽样的方法抽取2名第一组的学生共有6种等可能的结果,其中既有男生又有女生被抽中的有a1b1,a1b2,a2b1,a2b2这4种结果,得到概率.
(2)在这40名学生中按时间用分层抽样的方法抽取20名学生进行研究,得到每个个体被抽到的概率,根据概率相等写出比例式,得到要求的第二组要抽取的人数.
(3)本题是一个古典概型,试验发生事件是按时间用分层抽样的方法抽取2名第一组的学生共有6种等可能的结果,其中既有男生又有女生被抽中的有a1b1,a1b2,a2b1,a2b2这4种结果,得到概率.
解答:解:(1)根据频率,频数和样本容量之间的关系得到
s=
=0.2,
根据频率分布表中的所有的频率之和是1得到
t=1-0.1-s-0.3-0.25=0.15.
(2)设应抽取x名第一组的学生,
∴
=
,
得x=2.
故应抽取2名第一组的学生.
(3)由题意知本题是一个古典概型,
在(2)的条件下应抽取2名第一组的学生.
记第一组中2名男生为a1,a2,2名女生为b1,b2.
按时间用分层抽样的方法抽取2名第一组的学生共有6种等可能的结果,
列举如下:a1a2,a1b1,a1b2,a2b1,a2b2,b1b2.
其中既有男生又有女生被抽中的有a1b1,a1b2,a2b1,a2b2这4种结果,
∴既有男生又有女生被抽中的概率为P=
=
.
s=
| 8 |
| 40 |
根据频率分布表中的所有的频率之和是1得到
t=1-0.1-s-0.3-0.25=0.15.
(2)设应抽取x名第一组的学生,
∴
| x |
| 4 |
| 20 |
| 40 |
得x=2.
故应抽取2名第一组的学生.
(3)由题意知本题是一个古典概型,
在(2)的条件下应抽取2名第一组的学生.
记第一组中2名男生为a1,a2,2名女生为b1,b2.
按时间用分层抽样的方法抽取2名第一组的学生共有6种等可能的结果,
列举如下:a1a2,a1b1,a1b2,a2b1,a2b2,b1b2.
其中既有男生又有女生被抽中的有a1b1,a1b2,a2b1,a2b2这4种结果,
∴既有男生又有女生被抽中的概率为P=
| 4 |
| 6 |
| 2 |
| 3 |
点评:本题考查古典概型及其概率公式,考查频率,频数和样本容量之间的关系,考查分层抽样方法,在抽样过程中每个个体被抽到的概率相等,本题是一个概率与统计的综合题目.

练习册系列答案
相关题目
(本小题满分12分)
某校高三(1)班共有![]() 名学生,他们每天自主学习的时间全部在
名学生,他们每天自主学习的时间全部在![]() 分钟到
分钟到![]() 分钟之间,按他们学习时间的长短分
分钟之间,按他们学习时间的长短分![]() 个组统计得到如下频率分布表:
个组统计得到如下频率分布表:
| 分组 | 频数 | 频率 |
| [180 , 210) |
|
|
| [210 , 240) |
|
|
| [240 , 270) |
|
|
| [270 , 300) |
|
|
| [300 , 330) |
|
|
(1)求分布表中![]() ,
,![]() 的值;
的值;
(2)某兴趣小组为研究每天自主学习的时间与学习成绩的相关性,需要在这![]() 名学生中按时间用分层抽样的方法抽取
名学生中按时间用分层抽样的方法抽取![]() 名学生进行研究,问应抽取多少名第一组的学生?
名学生进行研究,问应抽取多少名第一组的学生?
(3)已知第一组的学生中男、女生均为![]() 人.在(2)的条件下抽取第一组的学生,求既有男生又有女生被抽中的概率.
人.在(2)的条件下抽取第一组的学生,求既有男生又有女生被抽中的概率.
 名学生,他们每天自主学习的时间全部在
名学生,他们每天自主学习的时间全部在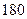 分钟到
分钟到 分钟之间,按他们学习时间的长短分
分钟之间,按他们学习时间的长短分 个组统计得到如下频率分布表:
个组统计得到如下频率分布表: 









 名学生进行研究,问应抽取多少名第一组的学生?
名学生进行研究,问应抽取多少名第一组的学生? 人.在(2)的条件下抽取第一组的学生,求既有男生又有女生被抽中的概率.
人.在(2)的条件下抽取第一组的学生,求既有男生又有女生被抽中的概率.


