题目内容
已知两个不共线的向量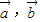 ,它们的夹角为θ,且
,它们的夹角为θ,且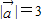 ,
,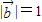 ,x为正实数.
,x为正实数.(1)若
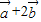 与
与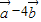 垂直,求tanθ;
垂直,求tanθ;(2)若
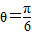 ,求
,求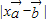 的最小值及对应的x的值,并判断此时向量
的最小值及对应的x的值,并判断此时向量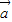 与
与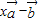 是否垂直?
是否垂直?
【答案】分析:(1)利用数量积运算、同角三角函数的基本关系式即可得出;
(2)利用数量积的性质和二次函数的单调性即可得出.
解答:解:(1)∵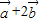 与
与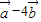 垂直,∴
垂直,∴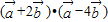 =0,
=0,
∴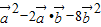 =0,
=0,
∴32-2×3×1×cosθ-8×12=0,∴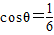 .
.
又θ∈(0,π),
∴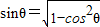 =
=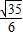 ,
,
∴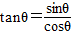 =
=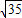 .
.
(2)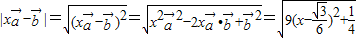 ,
,
故当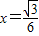 时,
时,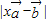 取得最小值为
取得最小值为 ,
,
此时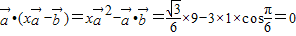 ,
,
故向量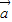 与
与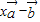 垂直.
垂直.
点评:熟练掌握数量积运算、同角三角函数的基本关系式、数量积的性质和二次函数的单调性是解题的关键.
(2)利用数量积的性质和二次函数的单调性即可得出.
解答:解:(1)∵
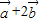 与
与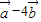 垂直,∴
垂直,∴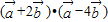 =0,
=0,∴
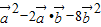 =0,
=0,∴32-2×3×1×cosθ-8×12=0,∴
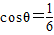 .
.又θ∈(0,π),
∴
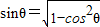 =
=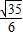 ,
,∴
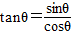 =
=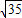 .
.(2)
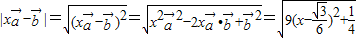 ,
,故当
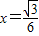 时,
时,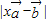 取得最小值为
取得最小值为 ,
,此时
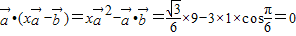 ,
,故向量
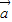 与
与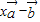 垂直.
垂直.点评:熟练掌握数量积运算、同角三角函数的基本关系式、数量积的性质和二次函数的单调性是解题的关键.

练习册系列答案
相关题目
已知两个不共线的向量a,b满足a+2xb=xa+yb,那么实数x,y的值分别是( )
| A、0,0 | B、1,2 | C、0,1 | D、2,1 |