题目内容
已知a为实数，f（x）=（x2﹣4）（x﹣a）．
（1）求导数f'（x）．
（2）若f'（﹣1）=0，求f（x）在[﹣2，2]上的最大值和最小值．
（3）若f（x）在（﹣∞，﹣2）和[2，+∞]上都是递增的，求a的取值范围．
（1）求导数f'（x）．
（2）若f'（﹣1）=0，求f（x）在[﹣2，2]上的最大值和最小值．
（3）若f（x）在（﹣∞，﹣2）和[2，+∞]上都是递增的，求a的取值范围．
解：（1）由原式得f（x）=x3﹣ax2﹣4x+4a，
∴f'（x）=3x2﹣2ax﹣4．
（2）由f'（﹣1）=0得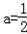
，
此时有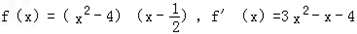
．
由f'（x）=0得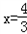
或x=﹣1，
又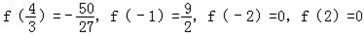
，
所以f（x）在[﹣2，2]上的最大值为
，最小值为
．
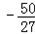（3）f'（x）=3x2﹣2ax﹣4的图象为开口向上且过点（0，﹣4）的抛物线，
由条件得f'（﹣2）≥0，f'（2）≥0，
∴﹣2≤a≤2．
所以a的取值范围为[﹣2，2]．
∴f'（x）=3x2﹣2ax﹣4．
（2）由f'（﹣1）=0得
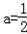，此时有
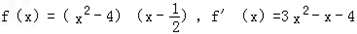．由f'（x）=0得
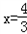或x=﹣1，又
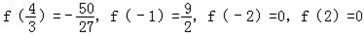，所以f（x）在[﹣2，2]上的最大值为
，最小值为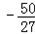．（3）f'（x）=3x2﹣2ax﹣4的图象为开口向上且过点（0，﹣4）的抛物线，
由条件得f'（﹣2）≥0，f'（2）≥0，
∴﹣2≤a≤2．
所以a的取值范围为[﹣2，2]．
练习册系列答案
相关题目