题目内容
某兴趣小组要测量电视塔AE的高度H(单位:m)如图所示,垂直放置的标杆BC的高度h=4m,仰角∠ABE=α,∠ADE=β.

(1)该小组已测得一组α、β的值,算出了tanα=1.24,tanβ=1.20,请据此算出H的值;
(2)该小组分析若干测得的数据后,认为适当调整标杆到电视塔的距离d(单位:m),使α与β之差较大,可以提高测量精度.若电视塔的实际高度为125m,试问d为多少时,α-β最大?

(1)该小组已测得一组α、β的值,算出了tanα=1.24,tanβ=1.20,请据此算出H的值;
(2)该小组分析若干测得的数据后,认为适当调整标杆到电视塔的距离d(单位:m),使α与β之差较大,可以提高测量精度.若电视塔的实际高度为125m,试问d为多少时,α-β最大?
(1)124m(2)55 m
m
 m
m(1)由 及AB+BD=AD,得
及AB+BD=AD,得 ,解得H=
,解得H= =124.
=124.
因此,算出的电视塔的高度H是124m.
(2)由题设知d=AB,得tanα= .
.
由AB=AD-BD= ,得tanβ=
,得tanβ= ,
,
所以tan(α-β)= ,
,
当且仅当d= ,即d=
,即d= =55
=55 时,上式取等号.所以当d=55
时,上式取等号.所以当d=55 时,tan(α-β)最大.因为0<β<α<
时,tan(α-β)最大.因为0<β<α< ,则0<α-β<
,则0<α-β< ,所以当d=55
,所以当d=55 时,α-β最大.故所求的d是55
时,α-β最大.故所求的d是55 m.
m.
 及AB+BD=AD,得
及AB+BD=AD,得 ,解得H=
,解得H= =124.
=124.因此,算出的电视塔的高度H是124m.
(2)由题设知d=AB,得tanα=
 .
.由AB=AD-BD=
 ,得tanβ=
,得tanβ= ,
,所以tan(α-β)=
 ,
,当且仅当d=
 ,即d=
,即d= =55
=55 时,上式取等号.所以当d=55
时,上式取等号.所以当d=55 时,tan(α-β)最大.因为0<β<α<
时,tan(α-β)最大.因为0<β<α< ,则0<α-β<
,则0<α-β< ,所以当d=55
,所以当d=55 时,α-β最大.故所求的d是55
时,α-β最大.故所求的d是55 m.
m.
练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目

 的值;
的值; 的值;
的值; 是第三象限角,求
是第三象限角,求 的值.
的值.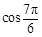 = .
= . =
=



 ,则
,则 .
. ( )
( )

 ,
, ,
, ,则
,则 的值_________.
的值_________. 的值是_______.
的值是_______.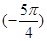 = .
= .