题目内容
18.已知函数f(x)=x2(x-a),其中a∈R.(1)若a=1,求曲线y=f(x)的过点(1,0)的切线方程.
(2)讨论函数y=f(x)在[0,4]上的单调性.
分析 (1)设出切点坐标是(m,m2(m-1),表示出切线方程,求出m的值,求出切线方程即可;
(2)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可.
解答 解:(1)a=1时,f(x)=x2(x-1),
f′(x)=2x(x-1)+x2=3x2-2x,
设切点坐标是:(m,m2(m-1),
则切线斜率k=3m2-2m,
故切线方程是:y-m2(m-1)=(3m2-2m)(x-m),
将(1,0)代入切线方程得:
-m2(m-1)=(3m2-2m)(1-m),
解得:m=0或m=1,
m=0时,切线方程是:y=0,
m=1时,切线方程是:x-y-1=0;
(2)f(x)=x2(x-a),
f′(x)=2x(x-a)+x2=3x2-2ax=x(3x-2a),
令f′(x)=0,解得:x=0或x=$\frac{2a}{3}$,
①$\frac{2a}{3}$≤0时,f′(x)≥0在[0,4]恒成立,
故f(x)在[0,4]递增,
②0<$\frac{2a}{3}$<4时,令f′(x)>0,解得:x>$\frac{2a}{3}$,
令f′(x)<0,解得:x<$\frac{2a}{3}$,
故f(x)在[0,$\frac{2a}{3}$)递减,在($\frac{2a}{3}$,4]递增,
③$\frac{2a}{3}$≥4时,f′(x)≤0在[0,4]恒成立,
故f(x)在[0,4]递减.
点评 本题考查了切线方程问题,考查函数的单调性问题,考查导数的应用以及分类讨论思想,是一道中档题.

练习册系列答案
相关题目
8.如图四个散点图中,适合用线性回归模型拟合其中两个变量的是( )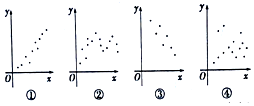

| A. | ①② | B. | ①③ | C. | ②③ | D. | ③④ |
 如图所示,在等腰梯形ABCD中,AD∥BC,AD=CD=AB=2,∠ABC=60°,将三角形ABD沿BD折起,使点A在平面BCD上的投影G落在BD上.
如图所示,在等腰梯形ABCD中,AD∥BC,AD=CD=AB=2,∠ABC=60°,将三角形ABD沿BD折起,使点A在平面BCD上的投影G落在BD上.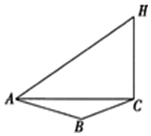 某烟花厂家为了测试最新研制出的一种“冲天”产品升空的安全性,特对其进行了一项测试.如图,这种烟花在燃放点C进行燃放实验,测试人员甲、乙分别在A,B两地(假设三地在同一水平面上),测试人员甲测得A、B两地相距80米且∠BAC=60°,甲听到烟花燃放“冲天”时的声音的时间比乙晚$\frac{1}{17}$秒.在A地测得该烟花升至最高点H处的仰角为60°.(已知声音的传播速度为340米∕秒)
某烟花厂家为了测试最新研制出的一种“冲天”产品升空的安全性,特对其进行了一项测试.如图,这种烟花在燃放点C进行燃放实验,测试人员甲、乙分别在A,B两地(假设三地在同一水平面上),测试人员甲测得A、B两地相距80米且∠BAC=60°,甲听到烟花燃放“冲天”时的声音的时间比乙晚$\frac{1}{17}$秒.在A地测得该烟花升至最高点H处的仰角为60°.(已知声音的传播速度为340米∕秒)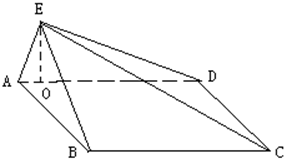 如图,正方形ABCD所在平面与三角形CDE所在平面相交于CD,AE⊥平面CDE,且AE=1,AB=2.
如图,正方形ABCD所在平面与三角形CDE所在平面相交于CD,AE⊥平面CDE,且AE=1,AB=2.