题目内容
函数f(x)=xα,对任意的x∈(-1,0)∪(0,1),若不等式f(x)>x恒成立,则在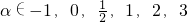 的条件下,α可以取的值的个数是
的条件下,α可以取的值的个数是
- A.4
- B.3
- C.2
- D.1
D
分析:由题设条件,分别把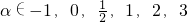 中的六个元素逐个代入f(x)=xα,逐个进行验正,能够得到α可以取的值的个数.
中的六个元素逐个代入f(x)=xα,逐个进行验正,能够得到α可以取的值的个数.
解答:当α=-1时,f(x)=x-1,
任意的x∈(-1,0)∪(0,1),
不等式f(x)>x不成立,
∴α≠-1;
当α=0时,f(x)=x0=1,
任意的x∈(-1,0)∪(0,1),
不等式f(x)>x不成立,
∴α≠0;
当α= 时,f(x)=x
时,f(x)=x ,
,
任意的x∈(-1,0)∪(0,1),
不等式f(x)>x不成立,
∴α≠ ;
;
当α=1时,f(x)=x,
任意的x∈(-1,0)∪(0,1),
不等式f(x)>x不成立,
∴α≠1;
当α=2时,f(x)=x2,
任意的x∈(-1,0)∪(0,1),
不等式f(x)>x不成立,
∴α≠2;
当α=3时,f(x)=x3,
任意的x∈(-1,0)∪(0,1),
不等式f(x)>x恒成立,
∴α=3.
综上所述,α可以取的值只有3.
故选D.
点评:本题考查幂函数的性质和应用,解题时要认真审题,注意采用逐个验正的方法能够得到答案.
分析:由题设条件,分别把
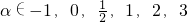 中的六个元素逐个代入f(x)=xα,逐个进行验正,能够得到α可以取的值的个数.
中的六个元素逐个代入f(x)=xα,逐个进行验正,能够得到α可以取的值的个数.解答:当α=-1时,f(x)=x-1,
任意的x∈(-1,0)∪(0,1),
不等式f(x)>x不成立,
∴α≠-1;
当α=0时,f(x)=x0=1,
任意的x∈(-1,0)∪(0,1),
不等式f(x)>x不成立,
∴α≠0;
当α=
 时,f(x)=x
时,f(x)=x ,
,任意的x∈(-1,0)∪(0,1),
不等式f(x)>x不成立,
∴α≠
 ;
;当α=1时,f(x)=x,
任意的x∈(-1,0)∪(0,1),
不等式f(x)>x不成立,
∴α≠1;
当α=2时,f(x)=x2,
任意的x∈(-1,0)∪(0,1),
不等式f(x)>x不成立,
∴α≠2;
当α=3时,f(x)=x3,
任意的x∈(-1,0)∪(0,1),
不等式f(x)>x恒成立,
∴α=3.
综上所述,α可以取的值只有3.
故选D.
点评:本题考查幂函数的性质和应用,解题时要认真审题,注意采用逐个验正的方法能够得到答案.

练习册系列答案
相关题目