题目内容
已知命题p:?x0∈R,使得ax02-2x0-1>0成立;命题q:函数y=loga(x+1)在区间(0,+∞)上为减函数;
(1)若命题¬p为真命题,求实数a的取值范围;
(2)若命题“p或q”为真命题,且“p且q”为假命题,求实数a的取值范围.
(1)若命题¬p为真命题,求实数a的取值范围;
(2)若命题“p或q”为真命题,且“p且q”为假命题,求实数a的取值范围.
(1)∵命题p:?x0∈R,使得ax02-2x0-1>0成立
∴¬p:?x∈R,ax2-2x-1≤0成立
∴①a≥0时ax2-2x-1≤0不恒成立
②由
得a≤-1
(2)∵命题q:函数y=loga(x+1)在区间(0,+∞)上为减函数
∴命题q为真,实数a的取值范围是:0<a<1
∵命题“p或q”为真,且“p且q”为假,
∴命题p、q一真一假
①当p真q假时,则
,得实数a的取值范围,-1<a≤0或a≥1
②当p假q真时,则
,实数a的取值范围:无解
∴实数a的取值范围是-1<a≤0或a≥1
∴¬p:?x∈R,ax2-2x-1≤0成立
∴①a≥0时ax2-2x-1≤0不恒成立
②由
|
(2)∵命题q:函数y=loga(x+1)在区间(0,+∞)上为减函数
∴命题q为真,实数a的取值范围是:0<a<1
∵命题“p或q”为真,且“p且q”为假,
∴命题p、q一真一假
①当p真q假时,则
|
②当p假q真时,则
|
∴实数a的取值范围是-1<a≤0或a≥1

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
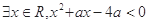 ”为假命题,是“
”为假命题,是“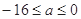 ”的( ).
”的( ).