题目内容
已知两个命题,命题甲:“直线y=kx+1与椭圆
+
=1恒有公共点”;命题乙:“方程
=x+a无实根”.若甲真乙假,求实数a的取值范围.
| x2 |
| 5 |
| y2 |
| a |
| x2-4 |
因为直线y=kx+1过定点(0,1),要使甲为真命题,则有1≤
且a≠5,解得a≥1且a≠5.
若乙为假命题,即方程
=x+a有实根,
设y=
,y=x+a,由y=
,得
-
=1(y≥0),作出它们的图象,由图象可知-2≤a<0或a≥2.
所以解得a≥2且a≠5.
所以实数a的取值范围是[2,5)∪(5,+∞)…(12分)
| a |
若乙为假命题,即方程
| x2-4 |
设y=
| x2-4 |
| x2-4 |
| x2 |
| 4 |
| y2 |
| 4 |
所以解得a≥2且a≠5.
所以实数a的取值范围是[2,5)∪(5,+∞)…(12分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
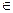 R,且
R,且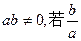 >1,则
>1,则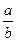 <1;
<1;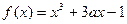 的零点时,第一次经计算
的零点时,第一次经计算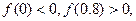 第二次应计算
第二次应计算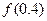 ;(2)线性相关系数
;(2)线性相关系数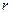 越大,两个变量的线性相关性越强;
越大,两个变量的线性相关性越强;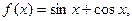 存在
存在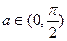 ,使
,使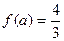 . 其中真命题为 .
. 其中真命题为 .