题目内容
已知数列{an},{bn}满足a1=2,2an=1+anan+1,bn=an-1,数列{bn}的前n项和 为Sn,Tn=S2n-Sn.
(Ⅰ)求证数列{ }是等差数列,并求数列{bn}的通项公式;
}是等差数列,并求数列{bn}的通项公式;
(Ⅱ)求证:Tn+1>Tn.
解:(1)由bn=an-1,得an=bn+1,代入2an=1+anan+1,
得2(bn+1)=1+(bn+1)(bn+1+1),
整理,得bnbn+1+bn+1-bn=0,
从而有 ,∵b1=a1-1=2-1=1,
,∵b1=a1-1=2-1=1,
∴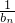 是首项为1,公差为1的等差数列,∴
是首项为1,公差为1的等差数列,∴ ,即
,即 .(5分)
.(5分)
(2)∵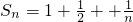 ,∴
,∴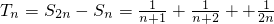 ,
,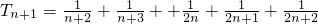 ,
,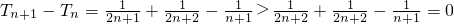 ,
,
(∵2n+1<2n+2)∴Tn+1>Tn.(12分)
分析:(1)将bn=an-1代入2an=1+anan+1,可得bn的递推关系式,整理变形可得 ,由等差数列的定义可得
,由等差数列的定义可得 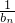 为等差数列,故可求其通项公式,进而求出bn.
为等差数列,故可求其通项公式,进而求出bn.
(2)结合(1)中的结论,写出Tn+1-Tn的表达式,利用放缩法证明该差大于0即可.
点评:本题考查了数列和不等式的综合应用,应用了构造法、放缩法、叠加法等数学思想方法,难度较大.
若根据2an=1+anan+1去求an 的通项,继而求bn,则难度很大.而应用了代入构造,避免了繁琐的中间计算过程.
得2(bn+1)=1+(bn+1)(bn+1+1),
整理,得bnbn+1+bn+1-bn=0,
从而有
 ,∵b1=a1-1=2-1=1,
,∵b1=a1-1=2-1=1,∴
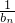 是首项为1,公差为1的等差数列,∴
是首项为1,公差为1的等差数列,∴ ,即
,即 .(5分)
.(5分)(2)∵
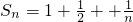 ,∴
,∴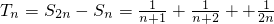 ,
,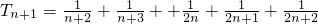 ,
,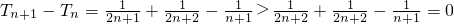 ,
,(∵2n+1<2n+2)∴Tn+1>Tn.(12分)
分析:(1)将bn=an-1代入2an=1+anan+1,可得bn的递推关系式,整理变形可得
 ,由等差数列的定义可得
,由等差数列的定义可得 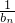 为等差数列,故可求其通项公式,进而求出bn.
为等差数列,故可求其通项公式,进而求出bn.(2)结合(1)中的结论,写出Tn+1-Tn的表达式,利用放缩法证明该差大于0即可.
点评:本题考查了数列和不等式的综合应用,应用了构造法、放缩法、叠加法等数学思想方法,难度较大.
若根据2an=1+anan+1去求an 的通项,继而求bn,则难度很大.而应用了代入构造,避免了繁琐的中间计算过程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目