题目内容
已知椭圆x2+
y2=a2(a>0)与A(2,1),B(4,3)为端点的线段没有公共点,则a的取值范围是( )
| 1 |
| 2 |
A、0<a<
| ||||||||
B、0<a<
| ||||||||
C、a<
| ||||||||
D、
|
分析:因为椭圆与线段无公共点,所以线段AB在椭圆的内部或在椭圆的外部,即由“A,B两点同在椭圆内或椭圆外”求解.
解答:解:根据题意有:A,B两点同在椭圆内或椭圆外
∴
或
∴0<a<
或a>
故选B
∴
|
|
∴0<a<
3
| ||
| 2 |
| ||
| 2 |
故选B
点评:本题主要通过直线与椭圆的位置关系,来考查点与椭圆的位置关系.当点(x0,y0)在椭圆
+
=1内,则有
+
<1,点(x0,y0)在椭圆
+
=1外,则有
+
>1
| x2 |
| a2 |
| y2 |
| b2 |
| x02 |
| a2 |
| y02 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| x02 |
| a2 |
| y02 |
| b2 |

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 (2012•长春模拟)已知椭圆
(2012•长春模拟)已知椭圆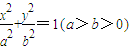 的左焦点为F1(-1,0),点F1关于直线16x+12y-9=0对称点在椭圆上.
的左焦点为F1(-1,0),点F1关于直线16x+12y-9=0对称点在椭圆上.
 的左焦点为F1(-1,0),点F1关于直线16x+12y-9=0对称点在椭圆上.
的左焦点为F1(-1,0),点F1关于直线16x+12y-9=0对称点在椭圆上.
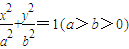 的左焦点为F1(-1,0),点F1关于直线16x+12y-9=0对称点在椭圆上.
的左焦点为F1(-1,0),点F1关于直线16x+12y-9=0对称点在椭圆上.