题目内容
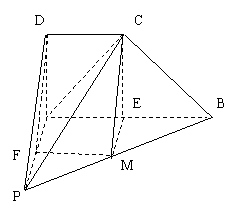
 (本小题12分)如图,在四棱锥P—ABCD中, CD∥AB, AD⊥AB, BC⊥PC ,
(本小题12分)如图,在四棱锥P—ABCD中, CD∥AB, AD⊥AB, BC⊥PC ,![]()
(1)求证:PA⊥BC
(2)试在线段PB上找一点M,
使CM∥平面PAD, 并说明理由.
(本小题12分)
解:1.连接AC,过C作CE⊥AB,垂足为E,
AD=DC,所以四边形ADCE是正方形。
 所以∠ACD=∠ACE=
所以∠ACD=∠ACE=![]() 因为AE=CD=
因为AE=CD=![]() AB,所以BE=AE=CE
AB,所以BE=AE=CE
![]() 所以∠BCE==
所以∠BCE==![]() 所以∠ACB=∠ACE+∠BCE=
所以∠ACB=∠ACE+∠BCE=![]()
所以AC⊥BC, …………………………………………………………… 3分
![]()
![]() 又因为BC⊥PC,AC∩PC=C,AC 平面PAC,PC 平面 PAC
又因为BC⊥PC,AC∩PC=C,AC 平面PAC,PC 平面 PAC
所以BC⊥平面 PAC,而 ![]() 平面 PAC,所以PA⊥BC. ………………… 6分
平面 PAC,所以PA⊥BC. ………………… 6分
2.当M为PB中点时,CM∥平面PAD, …………………………………… 8分
证明:取AP中点为F,连接CM,FM,DF.
则FM∥AB,FM=![]() AB,因为CD∥AB,CD=
AB,因为CD∥AB,CD=![]() AB,所以FM∥CD,FM=CD. ………9分
AB,所以FM∥CD,FM=CD. ………9分
所以四边形CDFM为平行四边形,所以CM∥DF, ……………………… 10分
因为DF![]() 平面PAD ,CM
平面PAD ,CM![]() 平面PAD,所以,CM∥平面PAD. ……………… 12分
平面PAD,所以,CM∥平面PAD. ……………… 12分

练习册系列答案
相关题目
 中,AC=BC, AC⊥BC,点D是A1B1中点.
中,AC=BC, AC⊥BC,点D是A1B1中点.  ,求二面角D- AC1-A1的余弦值.
,求二面角D- AC1-A1的余弦值.
 中,
中, 是边长为2的正三角形,且与底面垂直,底面
是边长为2的正三角形,且与底面垂直,底面 是
是 的菱形,
的菱形, 为
为 的中点.
的中点. 与底面
与底面 平面
平面 ;
; 的余弦值.
的余弦值. 
 中,底面
中,底面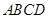 是正方形,
是正方形, ,
,  底面
底面 分别在
分别在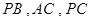 上,且
上,且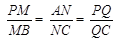
 ∥平面
∥平面 .
. 与平面面
与平面面

 平面BCD;
平面BCD;