题目内容
已知函数 (a∈R).
(a∈R).
(1)当a=3时,求函数f(x)的单调区间;
(2)若对于任意x∈[1,+∞)都有f'(x)<2(a-1)成立,求实数a的取值范围;
(3)若过点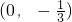 可作函数y=f(x)图象的三条不同切线,求实数a的取值范围.
可作函数y=f(x)图象的三条不同切线,求实数a的取值范围.
解:(1)当a=3时, ,得f'(x)=-x2+3x-2.…(1分)
,得f'(x)=-x2+3x-2.…(1分)
因为f'(x)=-x2+3x-2=-(x-1)(x-2),
所以当1<x<2时,f'(x)>0,函数f(x)单调递增;
当x<1或x>2时,f'(x)<0,函数f(x)单调递减.
所以函数f(x)的单调递增区间为(1,2),单调递减区间为(-∞,1)和(2,+∞).…(3分)
(2)方法1:由 ,得f'(x)=-x2+ax-2,
,得f'(x)=-x2+ax-2,
因为对于任意x∈[1,+∞)都有f'(x)<2(a-1)成立,
即对于任意x∈[1,+∞)都有-x2+ax-2<2(a-1)成立,
即对于任意x∈[1,+∞)都有x2-ax+2a>0成立,…(4分)
令h(x)=x2-ax+2a,
要使对任意x∈[1,+∞)都有h(x)>0成立,
必须满足△<0或 …(5分)
…(5分)
即a2-8a<0或 …(6分)
…(6分)
所以实数a的取值范围为(-1,8).…(7分)
方法2:由 ,得f'(x)=-x2+ax-2,
,得f'(x)=-x2+ax-2,
因为对于任意x∈[1,+∞)都有f'(x)<2(a-1)成立,
所以问题转化为,对于任意x∈[1,+∞)都有[f'(x)]max<2(a-1).…(4分)
因为 ,其图象开口向下,对称轴为
,其图象开口向下,对称轴为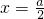 .
.
①当 时,即a<2时,f'(x)在[1,+∞)上单调递减,
时,即a<2时,f'(x)在[1,+∞)上单调递减,
所以f'(x)max=f'(1)=a-3,
由a-3<2(a-1),得a>-1,此时-1<a<2.…(5分)
②当 时,即a≥2时,f'(x)在
时,即a≥2时,f'(x)在 上单调递增,在
上单调递增,在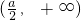 上单调递减,
上单调递减,
所以 ,
,
由 ,得0<a<8,此时2≤a<8.…Ks5u…(6分)
,得0<a<8,此时2≤a<8.…Ks5u…(6分)
综上①②可得,实数a的取值范围为(-1,8).…(7分)
(3)设点 是函数y=f(x)图象上的切点,
是函数y=f(x)图象上的切点,
则过点P的切线的斜率为k=f'(t)=-t2+at-2,…(8分)
所以过点P的切线方程为 .…(9分)
.…(9分)
因为点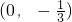 在切线上,
在切线上,
所以 ,
,
即 .…(10分)
.…(10分)
若过点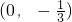 可作函数y=f(x)图象的三条不同切线,
可作函数y=f(x)图象的三条不同切线,
则方程 有三个不同的实数解.…(11分)
有三个不同的实数解.…(11分)
令 ,则函数y=g(t)与t轴有三个不同的交点.
,则函数y=g(t)与t轴有三个不同的交点.
令g'(t)=2t2-at=0,解得t=0或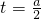 .…(12分)
.…(12分)
因为 ,
, ,
,
所以必须 ,即a>2.…Ks5u…(13分)
,即a>2.…Ks5u…(13分)
所以实数a的取值范围为(2,+∞).…(14分)
分析:(1)先求当a=3时函数的导数f′(x),并将其因式分解,便于解不等式,再由f′(x)>0,得函数的单调增区间,由f′(x)<0,得函数的单调减区间;
(2)方法1:由 ,得f'(x)=-x2+ax-2,原问题转化为:对于任意x∈[1,+∞)都有x2-ax+2a>0成立,令h(x)=x2-ax+2a,结合二次函数的性质得到关于a的不等关系,从而求出实数a的取值范围;
,得f'(x)=-x2+ax-2,原问题转化为:对于任意x∈[1,+∞)都有x2-ax+2a>0成立,令h(x)=x2-ax+2a,结合二次函数的性质得到关于a的不等关系,从而求出实数a的取值范围;
方法2:由 ,得f'(x)=-x2+ax-2,问题转化为,对于任意x∈[1,+∞)都有[f'(x)]max<2(a-1).下面利用导数工具研究其单调性和最大值,即可得出实数a的取值范围;
,得f'(x)=-x2+ax-2,问题转化为,对于任意x∈[1,+∞)都有[f'(x)]max<2(a-1).下面利用导数工具研究其单调性和最大值,即可得出实数a的取值范围;
(3)先将过点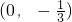 可作曲线y=f(x)的三条切线转化为:方程
可作曲线y=f(x)的三条切线转化为:方程 有三个不同的实数解,下面利用导数研究函数g(x)的零点,从而求得a的范围.
有三个不同的实数解,下面利用导数研究函数g(x)的零点,从而求得a的范围.
点评:本小题主要考查函数单调性的应用、利用导数研究曲线上某点切线方程、不等式的解法、函数恒成立问题等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.
 ,得f'(x)=-x2+3x-2.…(1分)
,得f'(x)=-x2+3x-2.…(1分)因为f'(x)=-x2+3x-2=-(x-1)(x-2),
所以当1<x<2时,f'(x)>0,函数f(x)单调递增;
当x<1或x>2时,f'(x)<0,函数f(x)单调递减.
所以函数f(x)的单调递增区间为(1,2),单调递减区间为(-∞,1)和(2,+∞).…(3分)
(2)方法1:由
 ,得f'(x)=-x2+ax-2,
,得f'(x)=-x2+ax-2,因为对于任意x∈[1,+∞)都有f'(x)<2(a-1)成立,
即对于任意x∈[1,+∞)都有-x2+ax-2<2(a-1)成立,
即对于任意x∈[1,+∞)都有x2-ax+2a>0成立,…(4分)
令h(x)=x2-ax+2a,
要使对任意x∈[1,+∞)都有h(x)>0成立,
必须满足△<0或
 …(5分)
…(5分)即a2-8a<0或
 …(6分)
…(6分)所以实数a的取值范围为(-1,8).…(7分)
方法2:由
 ,得f'(x)=-x2+ax-2,
,得f'(x)=-x2+ax-2,因为对于任意x∈[1,+∞)都有f'(x)<2(a-1)成立,
所以问题转化为,对于任意x∈[1,+∞)都有[f'(x)]max<2(a-1).…(4分)
因为
 ,其图象开口向下,对称轴为
,其图象开口向下,对称轴为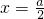 .
.①当
 时,即a<2时,f'(x)在[1,+∞)上单调递减,
时,即a<2时,f'(x)在[1,+∞)上单调递减,所以f'(x)max=f'(1)=a-3,
由a-3<2(a-1),得a>-1,此时-1<a<2.…(5分)
②当
 时,即a≥2时,f'(x)在
时,即a≥2时,f'(x)在 上单调递增,在
上单调递增,在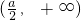 上单调递减,
上单调递减,所以
 ,
,由
 ,得0<a<8,此时2≤a<8.…Ks5u…(6分)
,得0<a<8,此时2≤a<8.…Ks5u…(6分)综上①②可得,实数a的取值范围为(-1,8).…(7分)
(3)设点
 是函数y=f(x)图象上的切点,
是函数y=f(x)图象上的切点,则过点P的切线的斜率为k=f'(t)=-t2+at-2,…(8分)
所以过点P的切线方程为
 .…(9分)
.…(9分)因为点
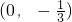 在切线上,
在切线上,所以
 ,
,即
 .…(10分)
.…(10分)若过点
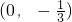 可作函数y=f(x)图象的三条不同切线,
可作函数y=f(x)图象的三条不同切线,则方程
 有三个不同的实数解.…(11分)
有三个不同的实数解.…(11分)令
 ,则函数y=g(t)与t轴有三个不同的交点.
,则函数y=g(t)与t轴有三个不同的交点.令g'(t)=2t2-at=0,解得t=0或
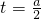 .…(12分)
.…(12分)因为
 ,
, ,
,所以必须
 ,即a>2.…Ks5u…(13分)
,即a>2.…Ks5u…(13分)所以实数a的取值范围为(2,+∞).…(14分)
分析:(1)先求当a=3时函数的导数f′(x),并将其因式分解,便于解不等式,再由f′(x)>0,得函数的单调增区间,由f′(x)<0,得函数的单调减区间;
(2)方法1:由
 ,得f'(x)=-x2+ax-2,原问题转化为:对于任意x∈[1,+∞)都有x2-ax+2a>0成立,令h(x)=x2-ax+2a,结合二次函数的性质得到关于a的不等关系,从而求出实数a的取值范围;
,得f'(x)=-x2+ax-2,原问题转化为:对于任意x∈[1,+∞)都有x2-ax+2a>0成立,令h(x)=x2-ax+2a,结合二次函数的性质得到关于a的不等关系,从而求出实数a的取值范围;方法2:由
 ,得f'(x)=-x2+ax-2,问题转化为,对于任意x∈[1,+∞)都有[f'(x)]max<2(a-1).下面利用导数工具研究其单调性和最大值,即可得出实数a的取值范围;
,得f'(x)=-x2+ax-2,问题转化为,对于任意x∈[1,+∞)都有[f'(x)]max<2(a-1).下面利用导数工具研究其单调性和最大值,即可得出实数a的取值范围;(3)先将过点
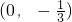 可作曲线y=f(x)的三条切线转化为:方程
可作曲线y=f(x)的三条切线转化为:方程 有三个不同的实数解,下面利用导数研究函数g(x)的零点,从而求得a的范围.
有三个不同的实数解,下面利用导数研究函数g(x)的零点,从而求得a的范围.点评:本小题主要考查函数单调性的应用、利用导数研究曲线上某点切线方程、不等式的解法、函数恒成立问题等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.

练习册系列答案
相关题目
 (a∈R且a≠0).
(a∈R且a≠0).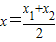 ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. (a∈R且a≠0).
(a∈R且a≠0). ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. (a∈R且a≠0).
(a∈R且a≠0). ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. ,a∈R.
,a∈R. 上的任意一个x,都有f(x)≤1成立,求a的取值范围.
上的任意一个x,都有f(x)≤1成立,求a的取值范围. (a∈R).
(a∈R). 在[1,e]上是增函数,求a的取值范围;
在[1,e]上是增函数,求a的取值范围;
 .
.